Wird eine Mathematikschulaufgabe geschrieben, so ergibt sich für jeden Schüler eine Note zwischen 1 und 6. Um Schulaufgaben einer Klasse im Jahresverlauf zu analysieren oder die gleiche Schulaufgabe in verschiedenen Klassen vergleichen zu können braucht man Aussagen über die Gesamtheit der Noten.
Dazu zählen insbesondere der Mittelwert und die Standardabweichung.
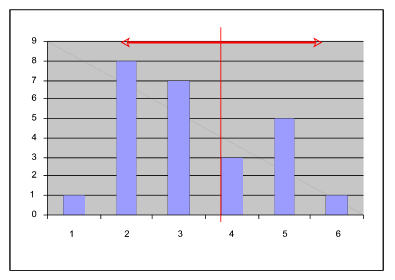
Beim Mittelwert (oder Durchschnitt) handelt es sich um die Summe aller Noten, geteilt durch deren Anzahl:
Mittelwert = (Note1 + Note2 + ... + NoteN) : N
Die Standardabweichung ergibt sich, indem man den Mittelwert aller Abweichungen bildet:
Standardabweichung = (Abweichung1 + Abweichung2 + ... + AbweichungN ) : N
Es wird von allen Abweichungen jeweils der Betrag genommen, sonst könnten sich negative mit positiven Abweichungen kompensieren.
Von Interesse ist oft auch noch die Zahl der Schüler, die eine bestimmte Note (z.B. eine 6) geschrieben haben. Solche Vorgänge werden der Statistik zugerechnet und die entsprechenden Algorithmen sollen hier kurz vorgestellt werden.
Um die Noten der Schulaufgaben aller Schüler einer Klasse zu speichern wird ein Feld benötigt.
int note[] = { 1, 3, 2, 3, 4, 4, 5, 6 };
8 Noten werden in einem Feld von ganzen Zahlen abgespeichert. Der Zugriff auf Einzelnoten erfolgt über die eckigen Klammern, will man z.B. auf das 2. Element des Feldes zugreifen, so schreibt man note[1] und erhält in diesem Fall eine 3. Das erste Element wird grundsätzlich mit note[0] referenziert.
Die Unterprogramme zur Berechnung von Mittelwert und Standardabweichung:
public static int summe( int feld[] ){ // zählt alle Zahlen aus feld zusammen
int s = 0; // Summe wird auf 0 gesetzt
for (int i=0; i < feld.length; i++ ){ // durch alle Zahlen durchmarschieren...
s+=feld[i]; // den Inhalt einer Zahl zur Summe addieren
}
return s; // Summe zurückgeben
}
public static double mittelwert( int feld[] ){
return summe( feld )/feld.length; // Mittelwert = Summe : Anzahl
}
public static double standard_abweichung( int feld[] ){
double mw = mittelwert( feld ); // in mw steht der Mittelwert
double summe_abweichung = 0; // Summe der Abweichungen ist erstmal 0
for ( int i = 0; i < feld.length; i++ ){ // durch alle Zahlen durchmarschieren
summe_abweichung+=Math.abs( feld[i] - mw ); // Abweichungen zur Summe dazuzählen
}
return summe_abweichung/feld.length; // Mittelwert der Abweichungen
}
public static void main(String args[]) {
int note[] = { 1, 3, 2, 4, 4, 5, 3, 6 };
System.out.println( "Notenschnitt: "+mittelwert( note ) );
System.out.println( "Standardabweichung: "+standard_abweichung( note ) );
}
Die Parameter für das jeweilige Unterprogramm sind sogenannte "offene Felder", d.h. die Länge des Feldes ist beim Übersetzen noch nicht bekannt und wird zur Laufzeit mit feld.length bestimmt.
Das Unterprogramm zur Berechnung der Anzahl einer bestimmten Note wird mittels des folgenden Quelltextes definiert:
public static int anzahl( int feld[], int wert ){
int zahl = 0;
for ( int i = 0; i < feld.length; i++ ){
if (feld[i] == wert) zahl++;
}
return zahl;
}
Zeichenketten werden dafür benötigt, Worte oder Sätze in einer Variablen oder Konstanten zu definieren. Sie verhalten sich ähnlich wie Felder, haben aber einige zusätzliche Eigenschaften, um die Arbeit mit dem Text zu erleichtern.
Hier ein Beispiel zur Erkennung, ob es sich bei einem eingegebenen Wort um ein "Palindrom" handelt (das ist ein Wort, welches vorwärts und rückwärts lesbar ist.
public static boolean checkPalindrom( String s ){ // Unterprogramm
for (int i = 0; i < s.length()/2; i++){ // erste Worthälfte scannen
// Überprüfung: Entspricht i.-ter Buchstabe dem i.-ten von hinten?
if (s.charAt(i) != s.charAt(s.length()-1-i)) return false; // ja dann gleich mit falsch beenden
}
return true; // alle Buchstaben übeprüft; es hat geklappt
}
public static void main(String args[]){
String s = InOut.readString();
if (checkPalindrom(s)) InOut.writeln( s+" ist ein Palindrom" );
else InOut.writeln( s+" ist kein Palindrom" );
}
"String" ist eine eigene Klasse in Java. Sie enthält sowohl die Zeichenkette selbst, als auch Unterprogramme zum Bearbeiten der Klasse. Hier einige Beispiele:
public char charAt(int i) |
Gibt das Zeichen zurück, welches sich an Position i in der Zeichenkette befindet. |
public int length() |
Gibt die aktuelle Länge der Zeichenkette zurück. |
public int indexOf( String s ) |
Gibt die Position zurück, an der sich s in der Zeichenkette befindet, sonst -1. |
public String replace( char oldChar, char newChar ) |
Gibt eine neue Zeichenkette zurück, in der alle Zeichen "oldChar" durch das Zeichen "newChar" ersetzt wurden. |
public String substring(int beginIndex) |
Gibt den Rest der Zeichenkette ab beginIndex zurück |
Ein spezieller Ausdruck in Java ist die Verwendung des Additionsopertors (+) zur Erzeugung und Verbindung von Zeichenketten. In den bisher gezeigten Beispielen gab es schon einige Zeilen der Art:
System.out.println( name+" ist "+jahre+" alt." );
Die Ausgabe dieser Zeile ist eine einfache Zeichenkette, in die die Variablenwerte von name und adjektiv eingefügt wurden. Der + Operator wird in Verbindung mit Zeichenketten als Verbindungszeichen verwendet. Variablen anderer primitiver Typen werden vorher in Zeichenketten umgewandelt und an die bestehende Zeichenkette angehängt. Auf diese Weise lassen sich sehr leicht Ausgabezeilen mit den verschiedensten Daten erzeugen.
Entschlüsseln Sie folgende Erkenntnis:
XFS EBTLJFTU, IBU'T LBQJFSU!
Satzzeichen und Hochkommata sind in diesem Fall unverschlüsselt.
Hier sollen drei einfache Methoden der Verschlüsselung vorgestellt werden:
- Alphabetisches Verschieben:
Die Zeichenkette wird im Alphabet um eine bestimmte Anzahl Buchstaben nach hinten verschoben.
| unverschlüsselte Buchstaben |
A B C D E F G H ... |
| verschlüsselte Buchstaben |
A B C D E F ... |
- Alphabetische Substitution:
Jedem Buchstaben wird eindeutig ein anderer des Alphabets zugeordnet. Das Alphabetische Verschieben gehört also auch zu den Substitutionen:
| unverschlüsselte Buchstaben |
A B C D E F G H ... |
| verschlüsselte Buchstaben |
B D Z A X F H G ... |
Der ganze Verschlüsselungsvorgang in einem Struktogramm:

- Transposition
Dieses Verfahren wurde schon 475 v. Christus eingesetzt. Ein Text wurde mehrzeilig auf einen langen rechteckigen Papierstreifen geschrieben und anschließend nach unten ausgelesen:
A |
L |
L |
E |
|
M |
E |
I |
N |
E |
E |
N |
T |
E |
N |
In verschlüsselter Form: AMELENLITENE EN.
Bei dem "LIFO"-Prinzip (Last-in-first-out) auch "Stack" oder "Keller" genannt, handelt es sich um eine Methode, gleichartige Daten nach dem Prinzip eines Stapels zu speichern.
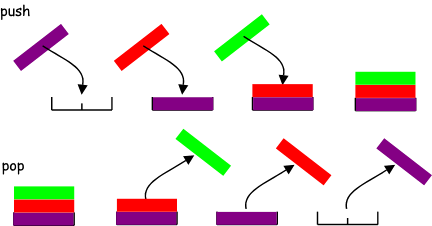
Am Anfang ist der Stapel leer. Werden nun Daten in den Stapel gelegt, so kommen sie "übereinander" zu liegen, d.h. erreichbar ist immer nur das Element, das als letztes "abgelegt" wurde. Um andere Elemente zu erreichen müssen zuerst die "darüberliegenden" entfernt werden.
Betrachten wir uns die zwei möglichen Aktionen als Struktogramm:
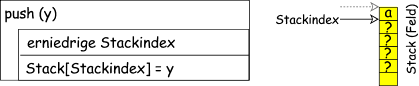
"push": Ablegen eines Elementes auf dem Stapel

"pop": Entnehmen eines Elementes vom Stapel
Um Daten von der Tastatur zu verarbeiten, werden die gedrückten Tasten vom Tastaturprozessor in der Reihenfolge, in der sie gedrückt wurden in einem kleinen Speicher (Tastaturpuffer) zwischengespeichert, bis sie vom Hauptprozessor weiterverarbeitet werden. Solche "Zwischenspeicher" zwischen einem "Erzeuger" und einem "Verbraucher" nennt man "FIFO" (First-in-first-out). Ihr Sinn ist es, den Datenaustausch zwischen zwei nicht synchronisierten Prozessen zu gewährleisten.
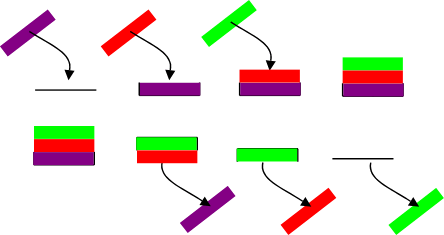
Wie läßt sich so eine Struktur mit einem Feld realisieren? Erzeuger und Verbraucher besitzen jeweils eine Variable die anzeigt, an welcher Position im Feld gerade geschrieben bzw. gelesen wird. Bei jeder Schreib- bzw. Leseoperation wird diese Variable um eins hochgezählt. Ist die Feldlänge überschritten, so wird wieder beim ersten Index begonnen (deshalt "Ring"-puffer). Ein Überlauf findet statt, wenn entwerder der Erzeuger das Feld voll geschrieben hat, oder der Leser es leergelesen hat.
Ein ganz anderes Beispiel zur Verwendung von Feldern sind zellulare Automaten. Dabei handelt es sich um ein Feld von "Zellen", die verschiedene Zustände (in unserem Fall Zahlenwerte oder "Farben") annehmen können. Bei jedem "Schritt" wird das komplette Feld neu berechnet, wobei jede Zelle ihren Zustand in Abhängigkeit von dem Zustand der Nachbarzellen ändert.
Die folgende Simulation mit zellularen Automaten kam in den 80er Jahren auf: Auf einer virtuellen Gitterebene leben "virtuelle Bakterien" nach einfachen Gesetzen. Das Wachstum hängt entscheidend von den umgebenden Zellen ab. Befinden sich rings um eine existierende "Bakterie" zwischen zwei und vier weitere, so bleibt sie am Leben ansonsten "verhungert" sie oder sie stirbt an Überbevölkerung. Befinden sich rings um eine freie Zelle drei Bakterien, so wird dort eine neue Zelle geboren.

Diese primitiven "Regeln" eines zweidimensionalen zellularen Automaten führen, je nach Ausgangssituation zu einem erstaunlich vielfältigen "Gewimmel" auf dem Bildschirm.
Zwei interessante Figuren seien hier noch vorgestellt:
- Die Ampel

Dies ist eine konstante Figur mit der Periode zwei. In jedem zweiten Schritt entstehen um den mittleren Punkt zwei neue während die alten zwei Randpunkte absterben.
- Der Gleiter

Dieses Gebilde "bewegt" sich mit Periode 4 durch den virtuellen Raum.
Hier folgt der Java-Quelltext für dieses Spiel:
class LifeWindow extends GraphicFrame{
private boolean Ebene[][]; // true bedeutet "Bakterie; false bedeutet "nix"
public void paint(Graphics g) { // wird aufgerufen, wenn Neuzeichnen ansteht
if (Ebene == null) return; // "Ebene" ist noch nicht mit Daten belegt
super.paint( g ); // Vorbereitungen
for (int i=0; i < Ebene.length; i++){ // alle y-Koordinaten
for (int j=0; j < Ebene[i].length; j++){ // alle x-Koordinaten
if (Ebene[i][j]) g.setColor( Color.black ); else g.setColor( Color.white );
g.fillRect( i*2, j*2, 2, 2 ); // zeichnet schwarz, wenn Bakterie vorhanden
}
}
}
public void setEbene( boolean neueEbene[][] ){ // die Bakterienkultur wird neu gesetzt
Ebene = new boolean[neueEbene.length][neueEbene[0].length]; // private Ebene wird neu definiert
for (int i=0; i < neueEbene.length; i++){ // alle y-Koordinaten
Ebene[i] = new boolean[neueEbene[i].length];
for (int j=0; j < neueEbene[i].length; j++){ // alle x-Koordinaten
Ebene[i][j] = neueEbene[i][j]; // Feld setzen
}
}
repaint(); // Neuzeichnen veranlassen
}
public void step(){ // Entwicklungsschritt der Kultur
if (Ebene == null) return; // noch keine "Daten" vorhanden.
boolean neueEbene[][] = new boolean[Ebene.length][Ebene[0].length]; //Ebene zum Zwischenspeichern
int anzahl; // Anzahl der umgebenden Bakterien
for (int i=1; i < Ebene.length-1; i++){ // für alle Punkte der Ebene...
for (int j=1; j < Ebene[i].length-1; j++){
anzahl = 0; // Anzahl ist erstmal 0
if (Ebene[i+1][j ]) anzahl++; // rechts
if (Ebene[i+1][j-1]) anzahl++; // rechts oben
if (Ebene[i ][j-1]) anzahl++; // links oben
if (Ebene[i-1][j-1]) anzahl++; // ...
if (Ebene[i-1][j ]) anzahl++;
if (Ebene[i-1][j+1]) anzahl++;
if (Ebene[i ][j+1]) anzahl++;
if (Ebene[i+1][j+1]) anzahl++;
neueEbene[i][j] = (Ebene[i][j] && (2 <= anzahl) && (anzahl <= 3)) // Bakterie überlebt
||(!Ebene[i][j] && ((anzahl == 3)) ); // .. wird geboren
}
}
// jetzt müssen die neuen Daten in das alte Feld geschrieben werden...
for (int i=1; i < Ebene.length-1; i++){
for (int j=1; j < Ebene[i].length-1; j++){
Ebene[i][j] = neueEbene[i][j];
}
}
repaint(); // Neuzeichnen veranlassen
}
}
class Life{
public static void main(String args[]) {
LifeWindow fenster = new LifeWindow();
boolean Ebene[][] = new boolean[80][80];
for (int i=60; i<63; i++) Ebene[i][39] = true;
for (int i=60; i<63; i++) Ebene[i][35] = true;
Ebene[50][50] = true;
Ebene[51][50] = true;
Ebene[52][50] = true;
Ebene[52][51] = true;
Ebene[51][52] = true;
fenster.setEbene( Ebene );
while (true){
fenster.step();
}
}
}








