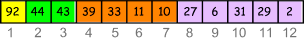Bubblesort arbeitet über den Austausch eines Elementes mit dem Nachbarelement und eignet sich deshalb gut als Einstieg in dieses Kapitel. Das Array wird dabei mehrmals durchlaufen und dabei wandert jedesmal das kleinste Element der restlichen Menge Richtung Startindex. Beispiel:
| 44 | 06 | 06 | 06 | 06 | 06 | 06 | 06 |
| 55 | 44 | 12 | 12 | 12 | 12 | 12 | 12 |
| 12 | 55 | 44 | 18 | 18 | 18 | 18 | 18 |
| 42 | 12 | 55 | 44 | 42 | 42 | 42 | 42 |
| 94 | 42 | 18 | 55 | 44 | 44 | 44 | 44 |
| 18 | 94 | 42 | 42 | 55 | 55 | 55 | 55 |
| 06 | 18 | 94 | 67 | 67 | 67 | 67 | 67 |
| 67 | 67 | 67 | 94 | 94 | 94 | 94 | 94 |
Der Name "Bubblesort" ergibt sich aus dem Wandern kleinerer (leichterer) Elemente (Blasen) zum kleineren Index hin (nach oben).

Dieser Algorithmus kann dadurch verbessert werden, dass man die äußere Schleife nicht komplett durchlaufen lässt (im Beispiel ändert sich in den letzten drei Abläufen nichts an der Reihenfolge), sondern dann aufhört, wenn kein Austausch mehr stattgefunden hat:
int a[] = { 44, 55, 12, 42, 94, 18, 6, 67 };
boolean tausch = true; // zeigt an, ob ein Tausch stattgefunden hat
int i = 1; int tmp; // Zähler und temporäre Variable
while (tausch) { // solange getauscht wurde
tausch = false; // erstmal wurde nichts getauscht
for (int j = a.length-1; j >= i; j--){ // von oben runter
if (a[j-1] > a[j]){ // stehen zwei Elemente in verkehrter Reihenfolge?
tmp = a[j-1]; a[j-1] = a[j]; a[j] = tmp; // dann tauschen
tausch = true; // ein Tausch hat stattgefunden
}
}
i++; // i kann eins erhöht werden, da bis i alles sortiert ist
for (int j=0; j<a.length; j++) System.out.print( a[j]+" " ); // Bildschirmausgabe
System.out.println();
}
Diese Methode wird meistens beim Kartenspiel eingesetzt. Die Elemente werden begrifflich in eine Ziel- und eine Quellensequenz aufgeteilt. Beginnend mit i=2 wird bei jedem Schritt das Element a[i] der Quellsequenz herausgegriffen und an der entsprechenden Stelle der Zielsequenz eingefügt. Anschließend wird i um 1 erhöht.
Erster Ansatz für den Algorithmus:
für i von 2 bis n
Setze x = a[i]
"füge x am entsprechenden Platz in a[1] bis a[i] ein"
ende für
Der Einfügealgorithmus sollte dann aus einem "nach links wandern" und "vergleichen" bestehen. Ist a[i] kleiner als das entsprechende a[j], so muss a[j] um eins nach rechts verschoben werden.
Zwei
Das Verfahren:
- Aussuchen des Elementes mit dem kleinsten Wert
- Austausch gegen das Element a[1]
- Erhöhen des kleinsten Index
Wurde vom enlischen Wissenschaftler C.A.R. Hoare vogeschlagen.
- Zerlege a in zwei Teilfelder a[1..k] und a[k+1..n] k ist willkürlich gewählt.
- Setze i=1 und j=n.
- Wiederhole bis i > j
- Suche mit i aufsteigend einen Wert größer a[k] und mit j absteigend ein Wert kleiner a[k]
- Tausche die Elemente a[i] und a[j] aus
- Sortiere die linke und rechte Seite nach dem gleichen Verfahren
Beispiel:
Start mit:
28 58 23 17 91 11 80 54
Wähle k = 3, also x = 23
28« 58 23 17 91 11 80 »54
i = 1 und j = 8;
a[i] ist größer als 23, i wird nicht verändert; j muss um zwei verkleinert werden: j = 6.
28« 58 23 17 91 »11 80 54
Austauschen der Elemente und weiterschieben von i und j:
11 58« 23 »17 91 28 80 54
Austauschen und fertig:
11 17 »23« 58 91 28 80 54
Im linken Feld befinden sich nun nur noch Werte kleiner 23 im rechten nur noch solche, die größer sind.
Anschließend werden
11 17 und 58 91 28 80 54
nach der gleichen Methode sortiert.
Das komplexeste Verfahren ist der Heapsort. Sein Vorteil ist, dass er selbst im schlimmsten Fall (worst case) noch sehr schnell ist. Der Heapsort arbeitet in zwei Schritten:
- Daten in eine bestimmte Struktur bringen
- Die vorstrukturierten Daten sortieren
1. Schritt: Daten in eine bestimmte Struktur bringen
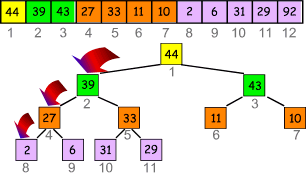
Der entscheidende Trick an dem Verfahren ist, dass man sich das Feld als binären Baum vorstellt. Dabei werden die Knoten Zeile für Zeile von oben nach unten durchnummeriert und ergeben so den Feldindex. Hier ein Beispiel mit einem unsortierten Feld:

Im hier beschriebenen ersten Schritt müssen die Daten so organisiert werden, dass an jeder Wurzel ein größeres Element steht als in den zugehörigen zwei Knoten darunter ("Heapstruktur"). Ein mögliches Beispiel für die oben genannten Zahlen:
Wie bringt man nun die komplett unsortierten Daten in eine Heapstruktur ("heapify")?
Man fängt in der vorletzten Zeile an (Feldlänge/2) und lässt die Elemente "versickern":
- Vergleiche das ausgesuchte Element mit den beiden darunterliegenden.
- Ist es das größte, dann passiert nichts weiter.
- sonst vertausche es mit dem größten darunterliegenden und versickere es von dieser Stelle aus weiter.
- Gehe zum nächstkleineren Index und fange von vorne an.
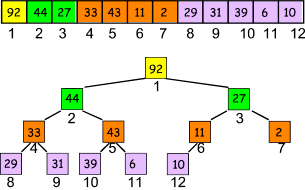
In unserem Beispiel:
- Berechne Feldlänge/2 => Erste Index ist 6.
- "Versickere" die 2: 11 ist größer als 2, also vertausche die beiden:
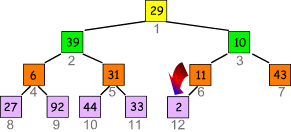
- Nächster Index ist 5
- "Versickere" die 31: 44 ist die größte Zahl, also vertausche die beiden:
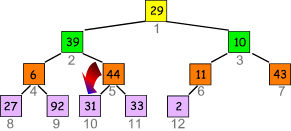
- Nächster Index ist 4
- "Versickere" die 6: 92 ist die größte Zahl, also vertausche die beiden:
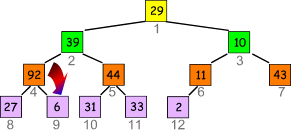
- Nächster Index ist 3
- "Versickere" die 10: 43 ist die größte Zahl, also vertausche die beiden:
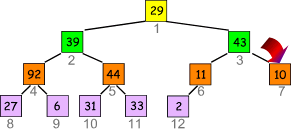
- Nächster Index ist 2
- "Versickere" die 39: 92 ist die größte Zahl, also vertausche die beiden:
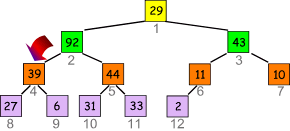
- An dieser Position ist die 39 größer als die beiden Unterknoten. Kein weiterer Tausch.
- Letzter Index ist 1
- "Versickere" die 29: Vertauschung mit 92, dann mit 44, dann mit 33:
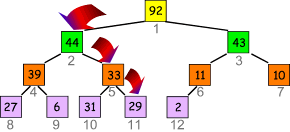
- Der entstandene Baum hat Heapstruktur; an jeder Position steht eine Zahl, deren Unterknoten kleiner sind.
Es entsteht also folgende Feldbelegung:
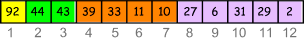
2. Schritt: Daten sortieren
In diesem Schritt geht man davon aus, dass das Feld (oder der gedachte entsprechende Baum) Heapstruktur besitzt.
Algorithmus:
- Wiederhole bis Baumgröße = 1
- Vertausche in der Liste das erste mit dem letzten Element.
- Verkürze den Baum um ein Element. (Das letzte Element im Feld ist bereits das größte).
- Versickere das neue erste Element in dem verkürzten Baum
public static void bubble( int a[] ){
boolean tausch;
int i = 1; int tmp;
do {
tausch = false;
for (int j = a.length-1; j >= i; j--){
if (a[j-1] > a[j]){
tmp = a[j-1]; a[j-1] = a[j]; a[j] = tmp;
tausch = true;
}
}
i++;
print( a );
} while (tausch);
}
public static void straightselection( int a[] ){
int min; int id; int tmp;
for (int j = 0; j < a.length-1; j++){
id = a.length; min = a[id-1]+1;
for (int i = a.length-1; i>=j; i--){
if (a[i] < min){
min = a[i]; id = i;
}
}
if (id < a.length){
tmp = a[j]; a[j] = a[id]; a[id] = tmp;
}
print( a );
}
}
public static void qsort( int a[], int first, int last ){
if (first >= last) return;
int k = (first+last)/2; int tmp;
int i = first; int j = last;
while (i < j){
while (a[i] < a[k]) i++;
while (a[j] > a[k]) j--;
tmp = a[i]; a[i] = a[j]; a[j] = tmp;
System.out.println( i+" "+j );
print( a );
}
qsort( a, first, k-1 );
qsort( a, k+1, last );
}