Ein Objekt heißt rekursiv, wenn es sich selbst enthält. In der Mathematik sind zum Beispiel rekursive Definitionen üblich.
-
0 ist eine natürliche Zahl
Addiert man 1 zu einer natürlichen Zahl so erhält man eine natürlche Zahl
-
Fakultät:
fak( n ) = n*fak( n-1 ); für n > 1
fak( n ) = 1; für 0 <= n <= 1
Die Fakultät lässt sich so kodieren:
public int fak( int n ){
if (n <= 1) return 1;
else return n*fak( n-1 );
}
Der größte gemeinsame Teiler zweier Zahlen a und b ist definiert als die größte ganze Zahl durch die sowohl a als auch b ohne Rest teilbar ist. Zum Beispiel ist der ggT( 42, 70 ) = 7. Ein Möglichkeit den ggT zu bestimmen besteht darin eine Primfaktorzerlegung der Zahlen durchzuführen. In diesem Fall ist das Produkt der gemeinsamen Primfaktoren der ggT:
42 = 2·3·7
70 = 2·5·7
ggT = 2·7 = 14
Ein wesentlich effizienterer Algorithmus ist der "Euklidische Algorithmus". Er gründet auf die Idee, dass der gemeinsame Teiler für a und b der gleiche ist, wie der von b und r, wobei r der Rest bei der Division von a durch b ist:
ggT(a,b) = ggT(b,r) mit r = a modulo b.
ggT( 70, 42 ) mit dem Euklidischen Algorithmus:
70 : 42 = 1 Rest 28
42 : 28 = 1 Rest 14
28 : 14 = 2 Rest 0
14 : 0 Ende
Im letzten Fall (Divisor 0) ist der Dividend das gesuchte Ergebnis.
Der rekursive Algorithmus dazu:
public static int ggT( int a, int b ){
if (b == 0) return a;
else return ggT( b, a % b );
}
Die Fibonacci-Reihe:
fib(n) = fib(n-1) + fib(n-2)
fib(2) = 1
fib(1) = 1
Die entstehende Reihe dazu:
1 1 2 3 5 8 13 21 ...
und der Quelltext dazu.
public int fib( int n ){
if (n <= 2) return 1;
else return fib( n-2 ) + fib( n-1 );
}
Verzweigende Rekursion ist sehr speicherintensiv, denn für jeden Unterprogrammaufruf müssen Daten im Speicher abgelegt werden und jede Ebene tiefer steigt die Zahl der Aufrufe exponentiell.
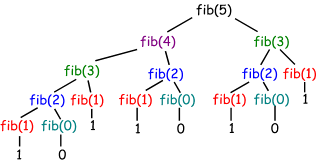
Hier kommt noch erschwerend hinzu, dass Unterprogramme zur Berechnung einer bestimmten Fibonaccizahl mehrfach im Speicher vorhanden sind. Die Berechnung von Fibonaccizahlen ist also auf diese Weise nicht sehr effizient.
In der Stochastik verwendet man für bestimmte Situationen der Kombinatorik das sogenannte Urnenmodell.
Dabei stellt man sich vor, dass sich mehrere Kugeln verschiedener Farben in einer "Urne" befinden. Welche Kombinationen sind möglich, wenn die Kugeln nacheinander ohne zurücklegen gezogen werden? Dabei lassen sich dann "Bäume" zeichnen, die die jeweiligen Züge nacheinander erfassen.
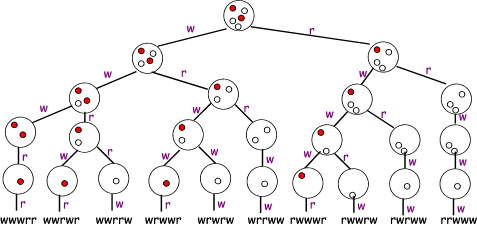
Da man die "leere" Urne ebenfalls als eine Belegung zulassen kann, bietet es sich an, alle Kombinationen wie folgt zu konstruieren:
- Ist die Urne leer?
Ausgabe der bisherigen Schritte
- sonst:
- Ziehen und Merken einer Kugel
- Wiederhole den Vorgang mit der Urne ohne die gezogene Kugel
Hier der Quelltext dazu:
class Rekursion {
public static String deleteCharAt( String s, int p ){
if (p == 0) return s.substring( 1 );
else return s.substring( 0, p )+s.substring( p+1 );
}
public static void traversiere_baum( String Pfad, String belegung ){
int p;
if ( belegung.length() == 0) InOut.writeln( Pfad );
else {
p = belegung.indexOf( 'w' );
if ( p >= 0) traversiere_baum( Pfad+"w", deleteCharAt( belegung, p ) );
p = belegung.indexOf( 'r' );
if ( p >= 0) traversiere_baum( Pfad+"r", deleteCharAt( belegung, p ) );
}
}
public static void main(String args[]){
String belegung = "wwwrr";
traversiere_baum( "", belegung );
}
}
Ein klassisches Beispiel für rekursive Lösung ist das Spiel "Die Türme von Hanoi". Dabei handelt es sich um drei Stangen, auf die Scheiben mit unterschiedlichem Durchmesser aufgesteckt werden können. Die einzige Bedingung ist, dass niemals eine Scheibe mit größerem Durchmesser auf einer mit kleinerem Durchmesser zu liegen kommt. Nun soll so ein "Turm" von Stange 1 nach Stange 3 verschoben werden.
Die Lösung für drei Scheiben schaut z.B. so aus:
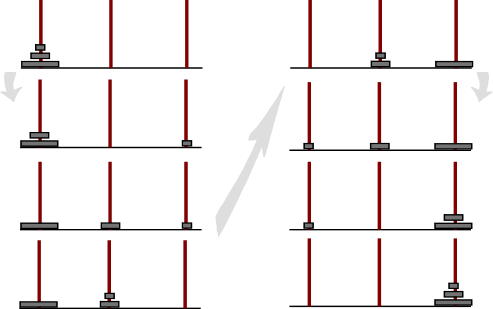
Man erkennt, dass man die unterste Scheibe nur dann bewegen kann, wenn die darüberliegenden auf die Stange 2 verschoben wurden. Also kann man die Lösung auch folgendermaßen formulieren:
Verschiebe einen Hanoi-Turm der Höhe n von Stange 1 nach Stange 3:
- Ist die Höhe n = 0, so mache gar nichts
- sonst:
- Verschiebe den Hanoi-Turm der Höhe n-1 auf Stange 2
- Verschiebe die verbleibende(unterste) Scheibe nach Stange 3
- Verschiebe den Hanoi-Turm der Höhe n-1 von Stange 2 nach Stange 3
Und hier noch etwas zum Tüfteln...

Dieses Muster wird durch eine immer feinere Überlagerung des folgenden Prinzips erzeugt:

Es handelt sich um einen rekursiven Aufruf von vier Unterprogrammen, die jeweils einen bestimmten Teil des Musters zeichnen. Die Unterprogramme wurden der Einfachheit halber von A bis D durchnummeriert. Hier der Grundalgorithmus der einzelnen Elemente:

Bei einem Aufruf in der nächsthöheren Ebene wird das zugrunde liegende Muster erweitert:
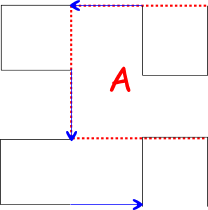
Ein Aufruf von A bewirkt also folgendes:
- Rufe D in der nächsthöheren Ebene auf
- Gehe um eine halbe Einheit nach links
- Rufe A in der nächsthöheren Ebene auf
- Gehe um eine halbe Einheit nach unten
- Rufe A in der nächsthöheren Ebene auf
- Gehe um eine halbe Einheit nach rechts
- Rufe B in der nächsthöheren Ebene auf
Und hier der Quelltext:
import java.awt.*;
import mygraphics.*;
class RRWindow extends GraphicFrame {
private int x, y;
private int h;
public void A(Graphics g, int i){
if (i > 0){
D(g,i-1); g.drawLine( x, y, x-h, y ); x=x-h;
A(g,i-1); g.drawLine( x, y, x, y-h ); y=y-h;
A(g,i-1); g.drawLine( x, y, x+h, y ); x=x+h;
B(g,i-1);
}
}
public void B(Graphics g, int i){
if (i > 0){
C(g,i-1); g.drawLine( x, y, x, y+h ); y=y+h;
B(g,i-1); g.drawLine( x, y, x+h, y ); x=x+h;
B(g,i-1); g.drawLine( x, y, x, y-h ); y=y-h;
A(g,i-1);
}
}
public void C(Graphics g, int i){
if (i > 0){
B(g,i-1); g.drawLine( x, y, x+h, y ); x=x+h;
C(g,i-1); g.drawLine( x, y, x, y+h ); y=y+h;
C(g,i-1); g.drawLine( x, y, x-h, y ); x=x-h;
D(g,i-1);
}
}
public void D(Graphics g, int i){
if (i > 0){
A(g,i-1); g.drawLine( x, y, x, y-h ); y=y-h;
D(g,i-1); g.drawLine( x, y, x-h, y ); x=x-h;
D(g,i-1); g.drawLine( x, y, x, y+h ); y=y+h;
C(g,i-1);
}
}
public void paint(Graphics g) {
super.paint( g );
h = 8;
C( g, 5 );
}
}
class Rekursion {
public static void main(String args[]){
System.out.println("Starting TestWindow...");
RRWindow fenster = new RRWindow();
}
}
- Was berechnet der Algorithmus, der durch den folgenden Quelltext dargestellt wird:
public static int foo ( int p, int q ){
if ( p == 0 ) return 0;
else return q*foo( p-1, q );
}
- Was berechnet der Algorithmus, der durch den folgenden Quelltext dargestellt wird:
public static int foo ( int p ){
if ( p = 1 ) return 1;
else return p + foo( p-1 );
}






