Angenommen, Sie schreiben ein Programm, bei dem an verschiedenen Stellen die Berechnung der Quadratwurzel benötigt wird. In diesem Fall müssten Sie jedesmal die Wurzel nach dem Heronverfahren berechnen, also an jeder entsprechenden Stelle im Programm die Initialisierung von x und die Schleife mit der Mittelwertbildung einfügen.

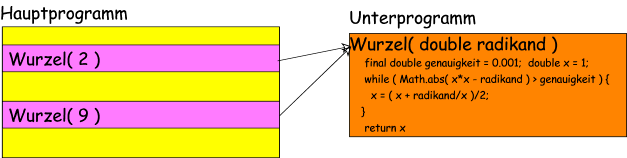
Dies kann man sich sparen, indem man sozusagen auf den Algorithmus zu Berechnung verweist, der sich an anderer Stelle im Quelltext befindet. Wird ein Teil des Programms auf diese Weise ausgelagert, so spricht man von einem Unterprogramm:
public static double quadratwurzel( double radikand ){
final double genauigkeit = 0.000001;
double x = 1;
while ( Math.abs( x*x - radikand ) > genauigkeit ) {
x = ( x + radikand/x )/2;
}
return x;
}
public static void main(String args[]) {
System.out.println( "Die Wurzel aus 2 ist: "+quadratwurzel( 2 ) );
System.out.println( "Die Wurzel aus 9 ist: "+quadratwurzel( 9 ) );
}
In diesem Beispiel wird das Unterprogramm "quadratwurzel" aus dem Programm "main" aufgerufen. Um die Wurzel aus unterschiedlichen Zahlen berechnen zu können, wurde der Radikand als "Parameter" übergeben.
Parameter sind Variablen, die speziell für den Aufruf des Unterprogramms erzeugt werden und danach nicht mehr existieren.
Mit Parametern hat man mehr Einfluss auf den Ablauf des Unterprogramms. Soll z.B. die Genauigkeit variieren, so kann man sie als zusätzlichen Parameter des Unterprogramms definieren:
public static double quadratwurzelgenau( double radikand, double genauigkeit ){
double x = 1;
while ( Math.abs( x*x - radikand ) > genauigkeit ) {
x = ( x + radikand/x )/2;
}
return x;
}
public static void main(String args[]) {
System.out.println( "Die Wurzel aus 2 ist: "+quadratwurzelgenau( 2, 0.01 ) );
System.out.println( "Die Wurzel aus 9 ist: "+quadratwurzelgenau( 9, 0.00000000000001 ) );
}
Unterprogramme können natürlich selbst wieder Unterprogrammaufrufe enthalten. In unserem Fall kann z.B. das Ausrechnen der Wurzel als Teil des allgemeineren Newton-Verfahrens zur Berechnung einer beliebigen ganzzahligen Wurzel gesehen werden:
Sucht man für die Funktion f(x) = x2 - a die Nullstelle, so erhält man genau die Wurzel aus a. Der Vorteil am Newtonverfahten ist aber, dass sich nun auch die 3.Wurzel berechnen lässt, indem man f(x) = x3 - a setzt.
Die Formel für die Newtoniteration einer beliebigen Funktion lautet übrigens:
xneu = xalt - f(xalt)/f'(xalt)
und wird in der folgenden Funktion wurzelgenau eingesetzt.
public static double potenz( double basis, int exp ){
int i; double faktor = basis;
if (exp == 0) return 1;
for (i = 2; i <= exp; i++){
basis = basis*faktor;
}
return basis;
}
public static double wurzelgenau( double radikand, int n, double genauigkeit ){
if (n < 2) return radikand;
double x = 1;
while( Math.abs( potenz( x, n ) - radikand ) > genauigkeit ){
x = x - (potenz( x, n ) - radikand)/(n*(potenz( x, n-1 ))); // Newtonverfahren
}
return x;
}
public static double quadratwurzelgenau( double radikand, double genauigkeit ){
return wurzelgenau( radikand, 2, genauigkeit );
}
public static double quadratwurzel( double radikand ){
return quadratwurzelgenau( radikand, 0.000001 );
}
public static double kubikwurzel( double radikand ){
return wurzelgenau( radikand, 3, 0.0000000001 );
}
public static void main(String args[]) {
System.out.println( "Die Wurzel aus 2 ist: "+quadratwurzel( 2 ) );
System.out.println( "Die 3.Wurzel aus 27 ist: "+kubikwurzel( 27 ) );
}
Hier kann man sehr schön sehen, wie sehr Unterprogramme die Universalität eines Programms erhöhen und gleichzeitig den Code vereinfachen.
Der hier entstandene Text kann schon als eine kleine Mathematikbibliothek gesehen werden.
Verfolgen wir nun den Aufruf der Kubikwurzel aus 27 zurück:
- kubikwurzel(27)
- wurzelgenau(27, 3, 0.0000000001)
- mehrmaliger Aufruf von potenz(3,3)
- Ergebnis in wurzelgenau: 3
- Ergebnis in kubikwurzel: 3
Die Verwendung von Unterprogrammen und der Einsatz von Parametern lässt sich auch sehr schön in Verbindung mit grafischen Ausgaben zeigen. Bei der Grafikausgabe wurde auch bisher schon ein Parameter verwendet.
Hier steht deshalb nochmals der Quelltext, den man benötigt um eine Linie in einem Fenster zu zeichnen:
package myprojects.testwindow;
import java.awt.*;
import mygraphics.*;
class RRWindow extends GraphicFrame {
public void paint(Graphics g) {
super.paint( g );
g.drawLine( 50, 0, 0, 100 );
}
}
class TestWindow {
public static void main(String args[]){
System.out.println("Starting TestWindow...");
RRWindow fenster = new RRWindow();
}
}
Die Klasse RRWindow ruft das Unterprogramm paint auf, um den Fensterinhalt zu zeichnen. Als Parameter wird die Klasse g vom Typ Graphics übergeben, die Befehle zum Zeichnen im Fenster enthält.
Deshalb bewirkt der Befehl g.drawLine das Zeichnen einer Linie im Fenster.
Durch einfügen von Befehlen in die paint-Routine kann deshalb der Fensterinhelt verändert werden.
Ziel des nächsten Abschnittes ist es, eine solche Figur zu erhalten:

Ein erster Ansatz das Haus zweimal zu zeichnen:
lass RRWindow extends GraphicFrame {
public void haus(Graphics graf){
graf.drawLine( 50, 0, 0, 100 );
graf.drawLine( 0, 100, 0, 200 );
graf.drawLine( 0, 200, 100, 200 );
graf.drawLine( 100, 200, 100, 100 );
graf.drawLine( 100, 100, 50, 0 );
}
public void paint(Graphics g) {
super.paint( g );
haus( g );
haus( g );
}
}
Hier wird das Haus zweimal gezeichnet, allerdings exakt an die gleiche Position:

Um das Haus an verschiedenen Positionen zeichnen zu können, muss also die Zeichenposition als Parameter übergeben werden:
public void hausXY(Graphics graf, int x, int y){
graf.drawLine( x+50, y+0, x+0, y+100 );
graf.drawLine( x+0, y+100, x+0, y+200 );
graf.drawLine( x+0, y+200, x+100, y+200 );
graf.drawLine( x+100, y+200, x+100, y+100 );
graf.drawLine( x+100, y+100, x+50, y+0 );
}
public void paint(Graphics g) {
super.paint( g );
hausXY( g, 0, 0 );
hausXY( g, 120, 120 );
}
Das Ergebnis ist schon vielversprechend, wir können aber die Größe des Hauses noch nicht verändern:

Dies ist nun der letzte Schritt:
public void hausXYS(Graphics graf, int x, int y, int s){
graf.drawLine( x+s/2, y+0, x+0, y+s );
graf.drawLine( x+0, y+s, x+0, y+s*2 );
graf.drawLine( x+0, y+s*2, x+s, y+s*2 );
graf.drawLine( x+s, y+s*2, x+s, y+s );
graf.drawLine( x+s, y+s, x+s/2, y+0 );
}
public void paint(Graphics g) {
super.paint( g );
int x, y, s;
for (int i=1; i < 20; i++){
x = (int)Math.round( 200*Math.random() );
y = (int)Math.round( 200*Math.random() );
s = (int)Math.round( 200*Math.random() );
hausXYS( g, x, y, s );
}
}



