erstes Anwenden des Zählprinzips, Veranschaulichen in Baumdiagrammen


Grundidee
Bestimmung der
  • Anzahl von Möglichkeiten bei
  • zusammengesetzten
  • Auswahlmöglichkeiten



Allgemeiner Fall
Zu jedem Schritt existiert eine Zahl von Auswahlmöglichkeiten, die nicht vom vorhergehenden Schritt abhängt.


Beispiel: Menü
In einem Menü gibt es 3 Vorspeisen, 4 Hauptspeisen und 2 Nachspeisen.
Zu jeder Vorspeise gibt es 4 Möglichkeiten für die Hauptspeise. Bei 3 Vorspeisen ergeben sich also 12 Kombinationen für Vor- und Hauptspeise.
Zu jeder Kombination hat man noch die Wahl unter 2 Nachspeisen. Insgesamt:
`N = 3*4*2 = 24`



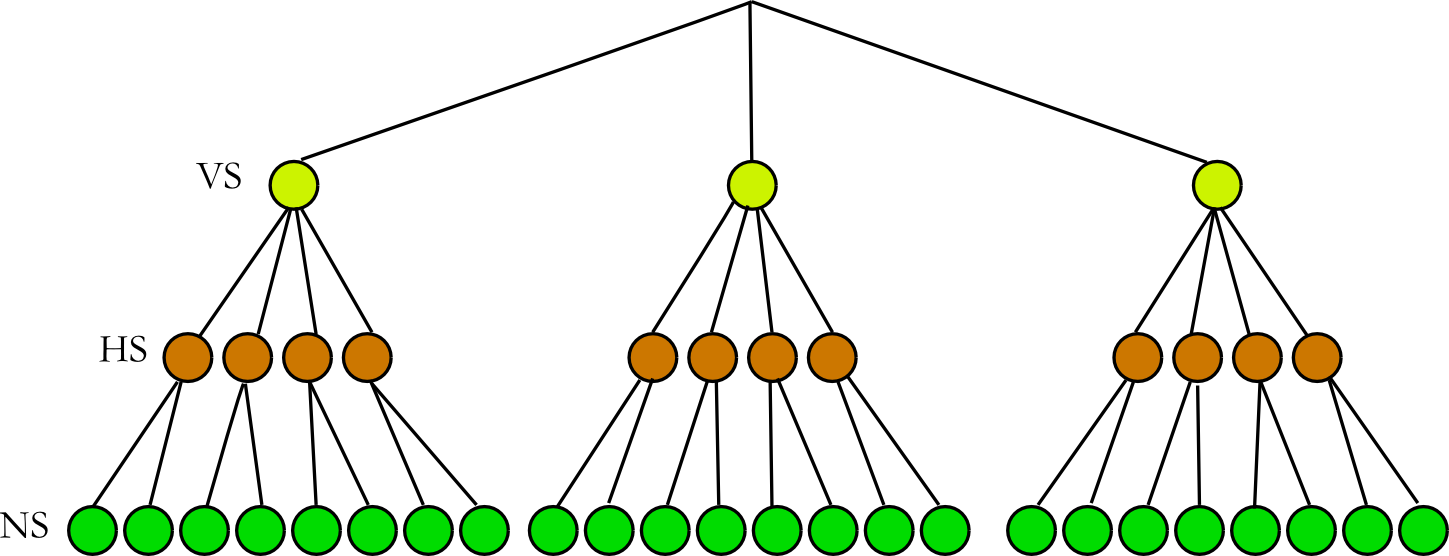
Baum: Menü mit 3 Vorspeisen (VS), 4 Hauptspeisen (HS) und 2 Nachspeisen (NS)

Spezialfall 1: immer die gleiche Auswahl
In jedem Schritt ist die Anzahl der Möglichkeiten gleich.


Beispiel: Bits im Computer
Für drei Bits ergeben sich
`N = 2*2*2 = 2^3 = 8` Möglichkeiten.



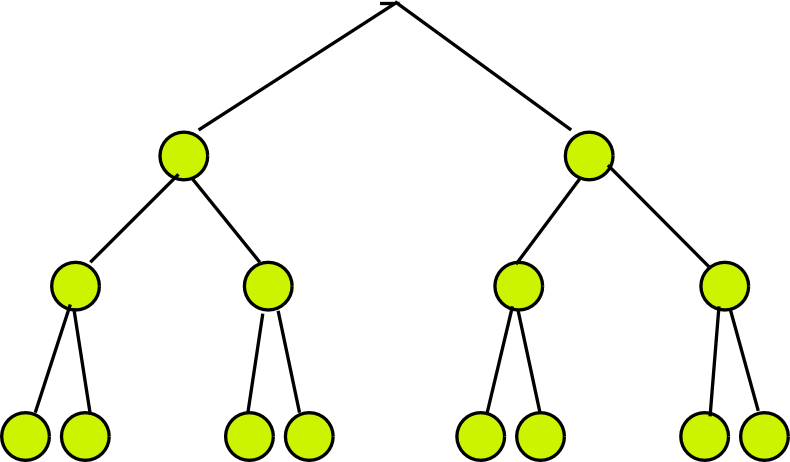
Baum: Besetzungsmöglichkeiten für 3 Bits im Computer

Spezialfall 2: Auswahl reduziert sich mit jedem Schritt um 1
Die Zahl der Auswahlmöglichkeiten beim ersten Schritt wird mit jedem Schritt um eins kleiner.


Beispiel: Freie Sitze
Wie viel Möglichkeiten ergeben sich, wenn man 2 Leute auf 4 freie Sitze verteilen möchte?
Der erste hat 4 Möglichkeiten sich hinzusetzen,
der zweite noch 3 Möglichkeiten.
`N = 4*3 = 12`



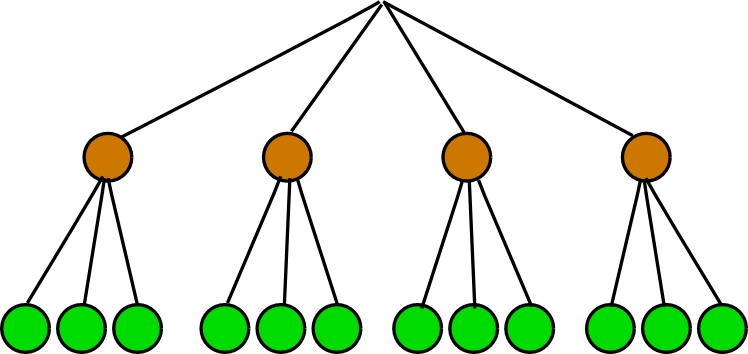
Baum: Zwei Leute auf vier freie Sitze