UHU-Startseite►Mathematik►Jahrgangsstufen►10►Exponentielles Wachstum und Logarithmen►Die allgemeine Exponentialfunktion►
Aufgaben (ohne Modellierung)


Spiegelung eines Funktionsgraphen
Gegeben ist die Exponentialfunktion `f : x |-> (1/3)^x (x in R)`.
  1. Zeichne den Graphen `G_f` der Funktion
  2. Zeichne den Graphen `G_g`, den man bei Spiegelung der Funktion an der y-Achse erhält
  3. Wie lautet die Funktionsgleichung g(x) = ... für die Funktion des gespiegelten Graphen?



Tipps zu "Spiegelung eines Funktionsgraphen"
  • für `f(x) = b*a^x` gilt, dass (Skalierung) `b = 1` und (Wachstum) `a=1/3`ist
  • beim Zeichnen des Graphens kann helfen, dass sich der y-Wert mit jedem Schritt nach rechts auf 33,3% verkleinert
  • zur Spiegelung an der y-Achse wird der horizontale Abstand des zu spiegelnden Punktes von der y-Achse verwendet
  • Um den Funktionsterm für `g(x) = b*a^x` zu bestimmen, wird die Skalierung und das Wachstum benötigt
  • Da der gespiegelte Graph die y-Achse ebenfalls bei 1 schneidet, besitzt er auch die Skalierung b = 1
  • Um das Wachstum von g(x) zu bestimmen, sollte man sich anschauen, wie sich f(x) entwickelt, wenn man einen Schritt rückwärts geht (warum?)



Veränderung einer Exponentialfunktion
Gegeben ist die Exponentialfunktion `f(x) = 2*(3/2)^x`
  1. Geben Sie den Definitionsbereich und den Wertebereich von f an
  2. Erstellen Sie eine Wertetabelle für ganzzahlige x mit −3 ≤ x ≤ 3 und zeichnen Sie damit den Graphen von f
  3. Wie ändert sich der Verlauf von f(x), wenn man b halbiert (Graph ohne Wertetabelle eintragen)
  4. Wie ändert sich der Verlauf von f, wenn man a halbiert (Graph ohne Wertetabelle eintragen)



Tipps zu "Veränderung einer Exponentialfunktion"
  • Definitionsbereich: alle Zahlen, die man für x einsetzen darf
  • Wertebereich: Menge aller Zahlen, die sich bei Eingabe aller x-Werte ergibt
  • Halbierung von b bedeutet die Skalierung zu halbieren; jeder Funktionswert liegt also nur noch halb so hoch
  • Halbierung bedeutet das Wachstum zu halbieren. Der Funktionswert für jeden nächsten Schritt wird also nur noch mit dem halben Wachstumsfaktor multipliziert



Zuordnen von Funktionstermen
Ordnen Sie den abgebildeten Funktionsgraphen jeweils eine der folgenden Funktionen zu:
  • `(2/3)^x`
  • `2*(1/3)^x`
  • `(1/2)^x+1`
  • `(3/2)^x`
  • `(1/3)^x`
  • `2^x+1`




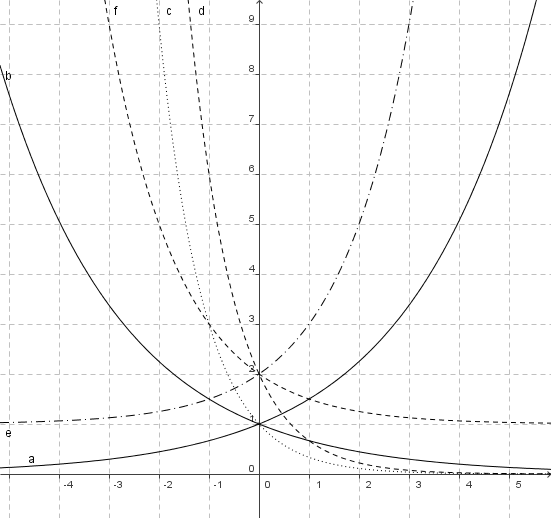
Graphen verschiedener Exponentialfunktionen
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion