Exponentialfunktion und Bruttoinlandsprodukt
| Mathematisches Modell der Entwicklung des BIP bei konstantem Wachstum |
- 2007 (Startzeitpunkt, x=0) beträgt das BIP 2.2 Billionen Euro
- das Wachstum beträgt über alle Jahre konstant 2,5%
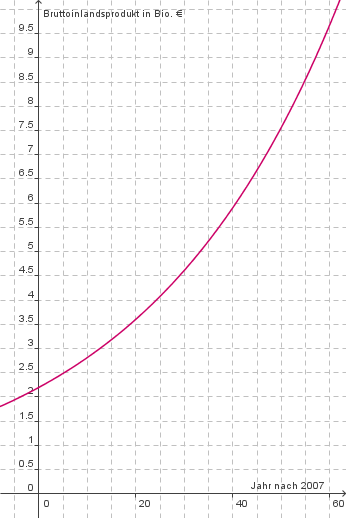
Entwicklung des BIP ab 2007 bei 2,5% Wachstum
| Funktionsterm |
-
Wachstum:
Von einem zum nächsten Jahr nimmt das BIP um 2.5% zu.
`=> BIP(x+1) = BIP(x) + BIP(x)*.025 = BIP(x)*1.025`
`=>` Addition in x-Richtung bedeutet Multiplikation in y-Richtung `=> BIP(x) = b*1.025^x` -
Skalierung:
Im Jahr 2007 lag das BIP bei 2.2 Bio €: `BIP(0) = 2.2 => BIP(x) = 2.2*1.025^x`
| Die allgemeine Exponentialfunktion |
Die allgemeine Exponentialfunktion f(x) zeichnet sich aus durch
`f(x) = b*a^x` mit `a, b in RR^"+"`
- das Wachstum a: `f(x+1) = a*f(x)` und
- die Skalierung b: `f(0) = b`
`f(x) = b*a^x` mit `a, b in RR^"+"`