UHU-Startseite►Mathematik►Jahrgangsstufen►10►Exponentielles Wachstum und Logarithmen►Die allgemeine Exponentialfunktion►
Exponentialfunktion, hergeleitet aus dem Bierschaumzerfall


Erweiterung des Definitionsbereiches
  1. Die Messung der Höhe des Bierschaumes hätte nicht unbedingt alle 20s, sondern zu jedem beliebigen Zeitpunkt erfolgen können.
  2. Für die beobachteten Versuche verhält sich der Bierschaum zu den Zeitpunkten als seine Höhe nicht gemessen wurde physikalisch genauso, wie während der Messung
  3. `=>` die Punkte dürfen zu einer Messkurve verbunden werden




0,83^x

Gültigkeit von Zahlen im Exponenten
Zur mathematischen Beschreibung muss
  1. der Definitionsbereich von f(x) auf `RR` erweitert werden
  2. geklärt werden, was z.B. `0.83^sqrt(2)` bedeutet



Irrationale Zahlen im Exponenten
  • Brüche im Exponenten lassen sich durch die Potenzgesetze zurückführen auf bekannte Zahldarstellungen: `a^(p/q) = (root q a)^p`
  • `sqrt 2` lässt sich durch Dezimalzahlen beliebig annähern
  • jede Dezimalzahl kann in einen Bruch `p/q` umgewandelt werden
  • `3^sqrt 2` kann auf dem gleichen Weg angenähert werden



Annäherung von `3^sqrt 2`
Im folgenden wird `sqrt 2` nach dem Heron-Verfahren angenähert:
SchrittNäherung für `sqrt 2`Näherung für `3^sqrt 2`
1 `2` `3^2 = 9`
2 `1.5` `3^(3/2) = (sqrt 3)^3 = 5.196`
3 `1.41667` `3^1.41667 = 4.742`
4 `1.41422` `3^1.41422 = 4.729`
5 `1.41421` `3^1.41421 = 4.729`
Der Wert ist also nach 5 Schritten schon auf 4 gültige Ziffern festgelegt.


Definition der Exponentialfunktion
Es sei `a in RR^"+"`. Dann heißt

`x|->a^x` mit `x in RR` Exponentialfunktion.




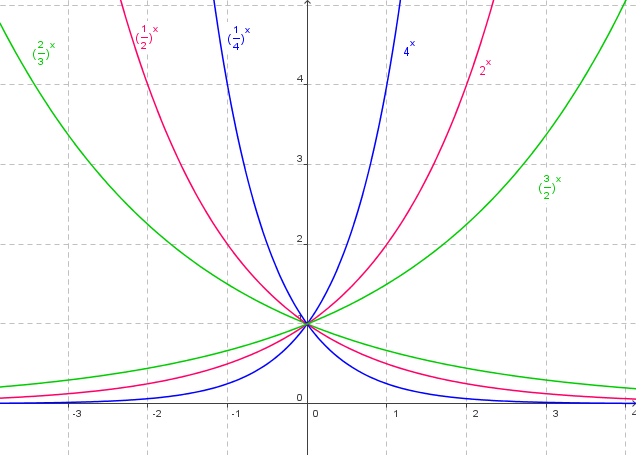
Verschiedene Exponentialfunktionen

Aufgabe I
Gegeben ist die Exponentialfunktion `x|->10^x; x in RR`.
  1. Setzt man für x nacheinander die Zahlen 0, 1, 2, ... ein, so erhält man eine Folge Funktionswerten. Wie erhält man aus einem Funktionswert den nächsten?
  2. Setzt man für x nacheinander die Zahlen 0, -1, -2, ... ein, so erhält man eine Folge Funktionswerten. Wie erhält man aus einem Funktionswert den nächsten?
  3. Wie hoch müsste ein Blatt sein (Einheit beider Achsen 1cm), wenn man den Graph der Funktion im Intervall [-10;+10] zeichnen wollte?



Aufgabe I, Tipp A
  1. Die ersten vier Funktionswerte sind:`1, 10, 100 und 1000`
  2. Die ersten vier Funktionswerte sind:`1, 1/10, 1/100 und 1/1000`
  3. Kleinster Funktionswert: `10^-10 cm`
    Größter Funktionswert `10^10cm`



Aufgabe I, Tipp B
  1. Der Quotient aus Folgewert und Wert ist konstant
  2. Der Quotient aus Folgewert und Wert ist konstant
  3. `10^-10 cm = 1 text(pm)`
    `10^10 cm = 10^8 m`



Aufgabe I, Lösung
  1. Multiplikation mit 10
  2. Division durch 10
  3. `10^8 m = 10^5 km = 100 000 km`
    `1 text(pm) ~~ 1/100` Durchmesser des Wasserstoffatoms



Aufgabe II
Wie ändert sich der Funktionswert der Exponentialfunktion `x|->a^x`, wenn man den x-Wert
  1. um 1 bzw 2 vergrößert
  2. um 1 verkleinert
  3. um 0.5 vergrößert
  4. verdoppelt
  5. halbiert



Aufgabe II, Tipp A
  1. `a^(x+1) = ` (Potenzgewetz anwenden)
  2. `a^(x-1) = ` (Potenzgewetz anwenden)
  3. `a^(x+0.5) = ` (Potenzgewetz anwenden)
  4. `a^(x*2) = ` (Potenzgewetz anwenden)
  5. `a^(x/2) = ` (Potenzgewetz anwenden)



Aufgabe II, Tipp B
  1. `a^(x+1)=a^x*a^1
  2. `a^(x-1)=a^x/a^1
  3. `a^(x+0.5)=a^x*a^0.5
  4. `a^(x*2)=(a^x)^2
  5. `a^(x/2)=(a^x)^(1/2)



Aufgabe II, Lösung
  1. Der Funktionswert wird mit a mutlipliziert
  2. Der Funktionswert wird durch a geteilt
  3. Der Funktionswert wird mit `sqrt a` mutlipliziert
  4. Der Funktionswert wird quadriert
  5. Aus dem Funktionswert wird die Wurzel gezogen
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion