UHU-Startseite►Mathematik►Jahrgangsstufen►6►Flächeninhalt geradlinig begrenzter Figuren►
Möglicher Lernpfad II


Buchstabenflächen
Man versetze sich in die Rolle eines Lampenherstellers, der Buchstaben ausleuchten soll. Jeder Quadratdezimeter des jeweils dargestellten Buchstabens soll eine Lampe bekommen.
Wieviele Quadratdezimeter müssen jeweils ausgeleuchtet werden und wieviele Lampen werden dann benötigt?


Das große I
Zur Gewöhnung: die Berechnung eines einfachen Rechtecks:
`A_R = g*h = 5 dm * 30 dm = 150 dm^2`



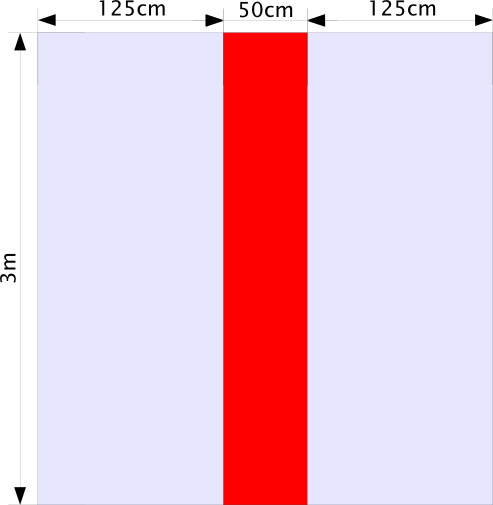
Das große I

Das große O
`A_O=2*5 dm * 30 dm + 2 * 5 dm * 20 dm = 500 dm²`



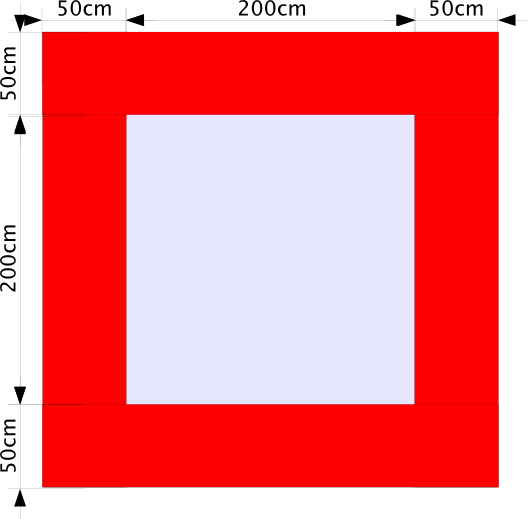
Das große O

Das große C
`A_C = A_O - 20dm * 5dm = 500 dm^2 - 100 dm^2 = 400 dm^2`



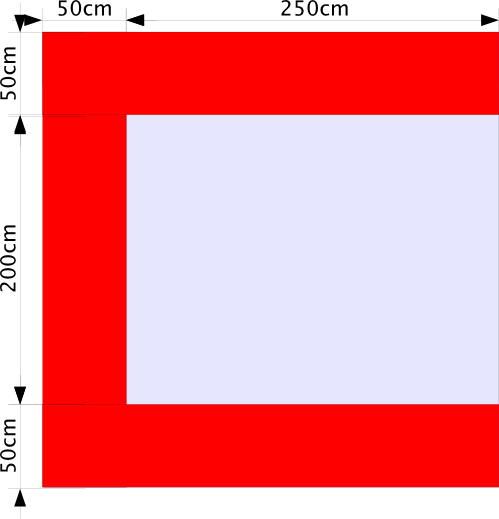
Das große C

Das große Z
Man zieht vom gesamten Flächeninhalt den Flächeninhalt der grauen Fläche ab: `A_Z = 30 dm * 30 dm - 20dm * 25 dm = 900 dm^2 - 500 dm^2 = 400 dm^2`
Frage: warum kommt hier der gleiche Flächeninhalt heraus wie beim C? Jetzt könnte man zum Beispiel über Scherung sprechen...



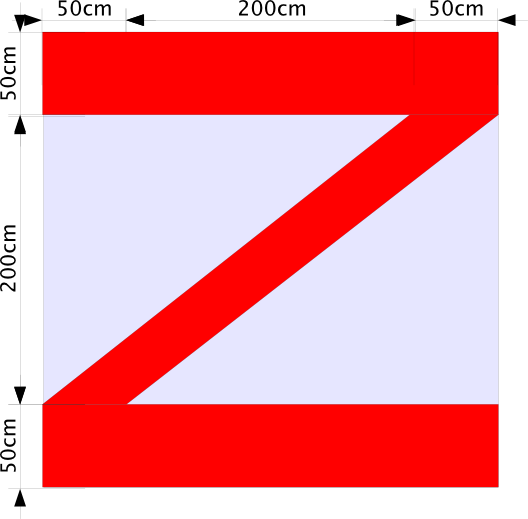
Das große Z

Rechteck-Parallelogramm
Die grauen (nicht-beleuchteten) Bereiche im Buchstaben C und im Buchstaben Z lassen sich immer zu einem Rechteck zusammensetzen, das den gleichen Flächeninhalt besitzt. Also "fehlt" beim C und beim Z in der Mitte gleichviel:
Wird eine Seite eines Rechtecks parallel zur gegenüberliegenden verschoben, so entsteht ein Parallelogramm.
zum Flächeninhalt:
Stimmen Rechteck und Parallelogramm in Grundlinie und Höhe überein, so besitzen sie die gleiche Fläche.




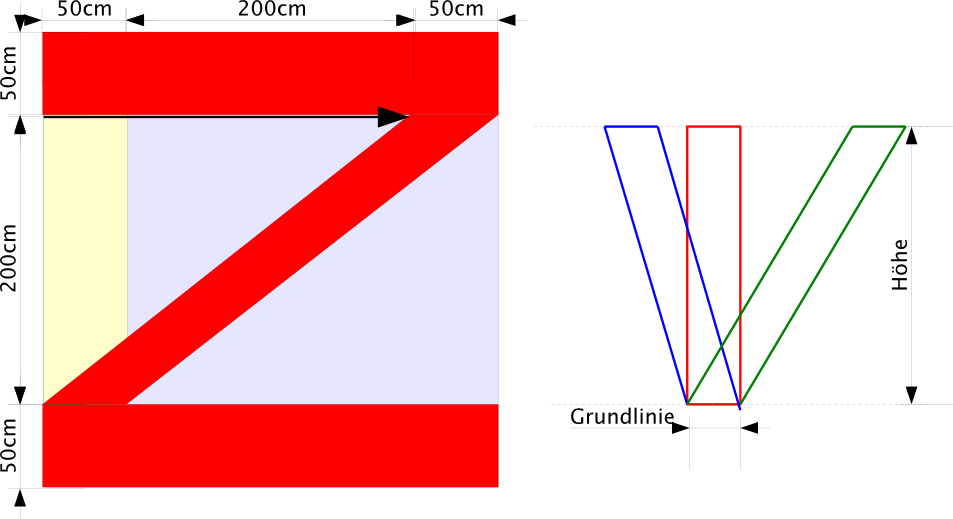
Scherung

Flächeninhalt des Parallelogramms
Der Flächeninhalt des Parallelogramms berechnet sich zu Grundlinie ⋅ Höhe.


optimal sichtbar mit Firefox Formeln mit asciimath Druckversion