UHU-Startseite►Mathematik►Jahrgangsstufen►7►Kongruenz►Kongruenzsätze für Dreiecke und grundlegende Konstruktionen►
Nicht-kongruente Dreiecke mit fünf übereinstimmenden Größen


5-con-Dreiecke nach "Mathematischer Zirkus":Martin Gardner
Die Dreiecke dürfen nicht in drei Seiten übereinstimmen, also stimmen sie in drei Winkeln überein, müssen also ähnlich sein.
Beispiel, sogar mit ganzzahligen Seitenlängen:
`a = 12; a' = 8;`
`b = 18; b' = 12;`
`c = 27; c' = 18;`
`alpha = alpha'; beta = beta'; gamma = gamma'`



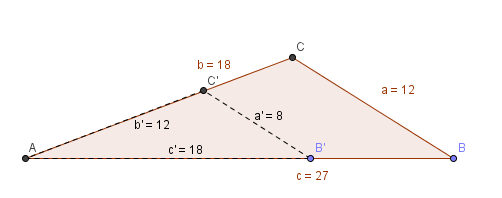
Zwei Dreiecke, die in 5 Größen übereinstimmen, aber nicht kongruent sind

Ideen dazu
Da `c' = b` und `b' = a` gelten muss, sind zwei Dreiecke zu suchen für die gilt:
`(c')/(b') = b/a` oder wegen der Ähnlichkeit von ABC und A'B'C':
`(c')/(b') = c/b = b/a`
Man muss also die kleinste Seite a' fortlaufend mit dem gleichen Faktor k multiplizieren um der Reihe nach b'=a, c'=b und c zu erhalten. Im Beispiel war der Faktor k = 1,5.
Anregungen:
  • Kann man einen beliebigen Faktor wählen? (Dreiecksgleichung!)
  • Wenn nicht, welches Intervall ist dann für k erlaubt?
  • Wie muss a' gewählt werden, damit alle Seiten natürliche Zahlen bleiben?
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion