Bestimmung des Kugelvolumens mit Hilfe des Cavalierischen Prinzips
| Vergleichskörper mit gleichem Flächenschnitt gesucht |
Achtung: Die zur Verfügung stehenden Modelle mit Bücherstapeln oder Ähnlichem zeigen nur den Spezialfall für kongruente Flächen auf gleicher Höhe, das Prinzip von Cavalieri gilt aber allgemeiner für gleiche Flächeninhalte (unabhängig von der Form!).
| Kugelschnitte |
- Jeder Schnitt durch eine Kugel ist ein Kreis.
- Entscheidend für den Radius dieses Kreises ist der Abstand des Kreismittelpunktes vom Kugelmittelpunkt
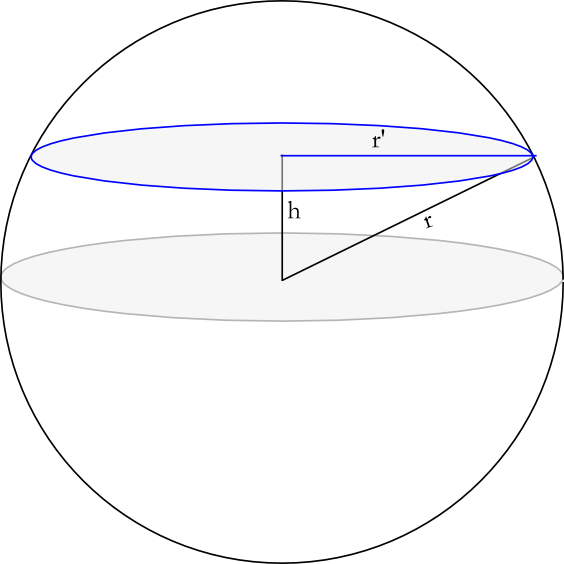
Kleinkreis einer Kugel mit Abstand h vom Zentrum
| Bestimmung des Schnittflächeninhaltes |
`A_S = pi*(r^2-h^2)` (Pythagoras)
`A_S = pi*r^2 - pi*h^2`
- Da r der Radius der Kugel ist, bleibt der erste Minuend konstant, während der Subtrahend linear mit der Höhe zunimmt.
- Minuend und Subtrahend lassen sich selbst als Term für den Inhalt eines Kreises deuten.
- Die Differenz lässt sich dann als Fläche eines "Kreisrings" interpretieren.
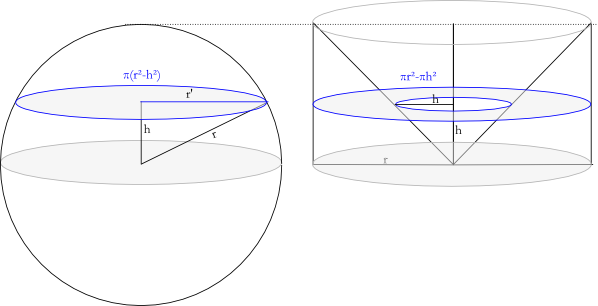
Vergleich Kugelvolumen mit kegelförmig ausgehöhltem Zylinder
| Kugelvolumen mit Hilfe des Vergleichskörpers |
`V_text(Halbkugel) = V_text(Zylinder) - V_text(Kegel) = pi*r^2*r - 1/3 pi*r^2*r = 2/3 pi r^3`
Kugelvolumen:
`V = 4/3 pi r^3`
| Applet zum Thema |