Einführung des Tangens


Definition der Steigung
Die Steigung einer Geraden ist definiert als:
`m = (Delta y)/(Delta x) text( )`   (Hochwertunterschied/Rechtswertunterschied)


Steigung der Hypothenuse eines rechtwinkligen Dreiecks im Einheitskreis
Wie groß ist die Steigung im Einheitskreis, wenn der Winkel α bekannt ist?



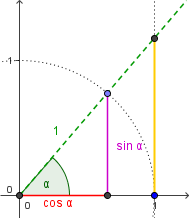
Steigung im Einheitskreis

`m = (Delta y)/(Delta x) = (sin alpha)/(cos alpha)`.


Geometrische Darstellung der Steigung
  • Über ähnliche Dreiecke lässt sich folgendes Erkennen:
  • `(sin alpha)/(cos alpha) = text(Länge gelbe Strecke)/1 = text(Länge gelbe Strecke)`
  • Die Länge der gelben Strecke zeigt also die Steigung an, die durch den Winkel α festgelegt wird
  • Den Wert der Steigung erhält man, indem man die Tangente am Einheitskreis mit dem freien Schenkel des Winkels schneidet
  • Die so definierte Steigung zu Winkel α nennt man `tan alpha`.



Definition
Der Tangens eines Winkels α ist definiert als:
  • die Steigung der Geraden, die die x-Achse im Winkel α schneidet
  • die Länge der Tangentenstrecke zwischen (1;0) und dem Schnittpunkt des freien Schenkels des Winkels mit dem Einheitskreis
  • dem Term `tan alpha = (sin alpha)/(cos alpha)



Einfache Aufgaben
  1. Ohne Taschenrechner: Wie groß ist der Tangens von 0°, 30°, 45°, 60° und 90°?
  2. Wie hoch ist ein 4200m entfernter Fernsehturm, wenn er unter 10° zum Horizont erscheint?
  3. Welche Neigung hat eine schiefe Ebene, wenn die Hangabtriebskraft eines Körpers 2300N und die Normalkraft 8600N beträgt? Welche Masse hat dieser Körper?