UHU-Startseite►Mathematik►Jahrgangsstufen►9►Stochastik: Zusammengesetzte Zufallsexperimente►
Pfadregeln und ihre Anwendung


1. Pfadregel
Die Wahrscheinlichkeit eines Elementarereignisses in einem mehrstufigen Zufallsexperiment ist gleich dem Produkt der Wahrscheinlichkeiten auf dem Pfad, der zu diesem Elementarereignis führt.



2. Pfadregel
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Pfade, die zu diesem Ereignis führen.



Das Ziegenproblem nach "Das Ziegenproblem; Denken in Wahrscheinlichkeiten":Gero von Randow
In einer Show kann ein Kandidat zwischen drei Türen wählen. Hinter einer befindet sich ein Auto, hinter den anderen beiden jeweils eine Ziege. Wenn sich der Kandidat für eine Tür entschieden hat, öffnet der Moderator ihm eine Tür mit einer Ziege. Soll der Kandidat die Tür wechseln, oder bei seiner Tür bleiben?
Im folgenden Bamdiagramm steht das Auto hinter der Tür A und der Kandidat entscheidet sich völlig unbedarft (hat also nicht diese Seite gelesen). Das Diagramm ist folgendermaßen zu lesen:
  • Der Kandidat entscheidet sich für Tür A, B oder C
  • Da der Moderator weiß, hinter welcher Tür sich das Auto befindet, entscheidet er sich, abhängig von der gewählten Tür des Kandidaten für eine Tür mit Ziege.
    Nimmt der Kandidat z.B. Tür B, so kann der Moderator nur noch Tür C öffnen (Wahrscheinlichkeit 1)
  • Im dritten Schritt kann sich der Kandidat dafür entscheiden, die Tür zu wechseln, oder bei seiner Tür zu bleiben.
  • Bei Durchwanderung jedes Pfades erhält man alle Möglichkeiten, die sich ergeben, wenn sich das Auto hinter A befindet. Die Wahrscheinlichkeit für die entsprechende Wahl ergibt sich aus dem Produkt der einzelnen Pfadwahrscheinlichkeiten.
  • Im letzten Schritt vergleicht man die Summe der Wahrscheinlichkeiten für den Fall beim Türwechsel zu verlieren und die Summe der Wahrscheinlichkeiten für den Fall beim Türwechsel zu gewinnen.




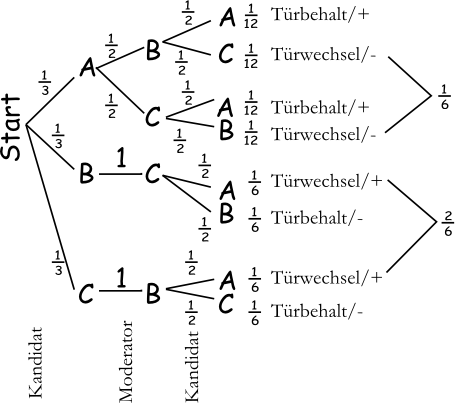
Baumdiagramm zum Ziegenproblem

Technische Redundanz beim Fallschirmspringen nach "Das Ziegenproblem; Denken in Wahrscheinlichkeiten":Gero von Randow
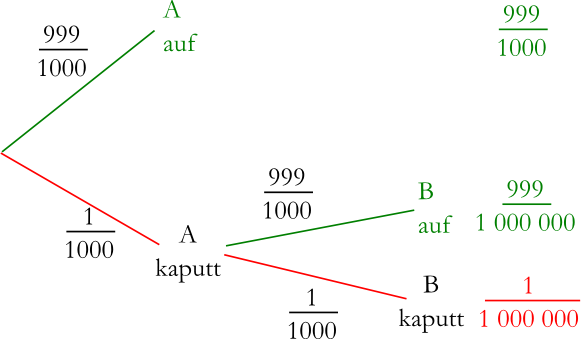
Die Wahrscheinlichkeit dafür, dass sich ein Fallschirm nicht öffnet, liegt etwa bei ` P(bar F) = 1/1000 `. Ein Fallschirmspringer springt normalerweise mit zwei Schirmen ab. Wie groß ist die Wahrscheinlichkeit, dass sich keiner von beiden Schirmen öffnet?



Zwei Fallschirme
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion