Beweise



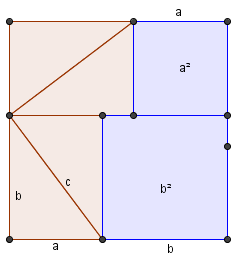
Quadrat der Seitenlänge a+b anders zusammengesetzt

Beweise mit ein Quadrat der Seitenlänge a+b
  1. Ergänzungsgleichheit
  2. Algebraischer Vergleich




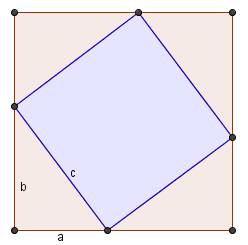
Quadrat mit a + b

1. Ergänzungsgleichheit
Die braunen Dreiecke werden mit nun so neu zusammengelegt, dass ebenfalls ein Quadrat der Seitenlänge a+b entsteht:


2. Algebraischer Vergleich
Berechnung des Flächeninhalts:
Gesamtfläche ist Fläche der 4 rechtwinkligen Dreiecke zusammen mit der inneren Quadratfläche:
`(a+b)^2 = 4*(1/2*a*b) + c^2`
`a^2 + 2ab + b^2 = 2ab + c^2`
`a^2 + b^2 = c^2`



Beweis über Scherung
Bei dieser Methode steht die Prozessorientierung im Vordergrund.
  • Kurz die Scherung wiederholen
  • Scherung mit DGS vorführen, oder Animation
  • Kathetensätze werden hier gleich mitbewiesen




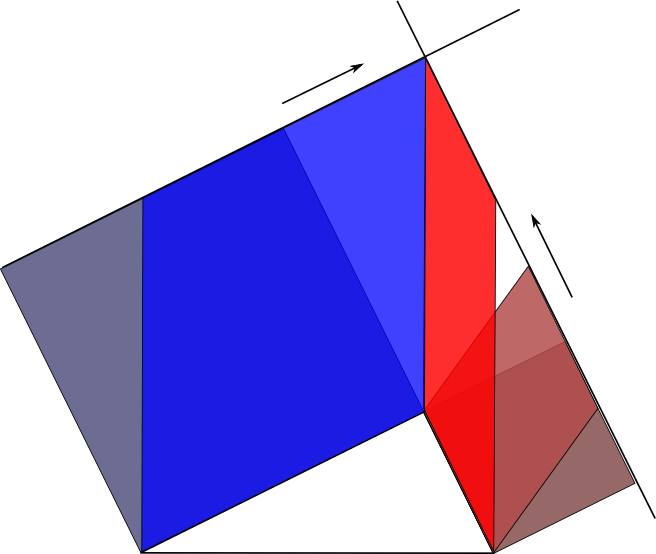
Scherung I


Scherung II


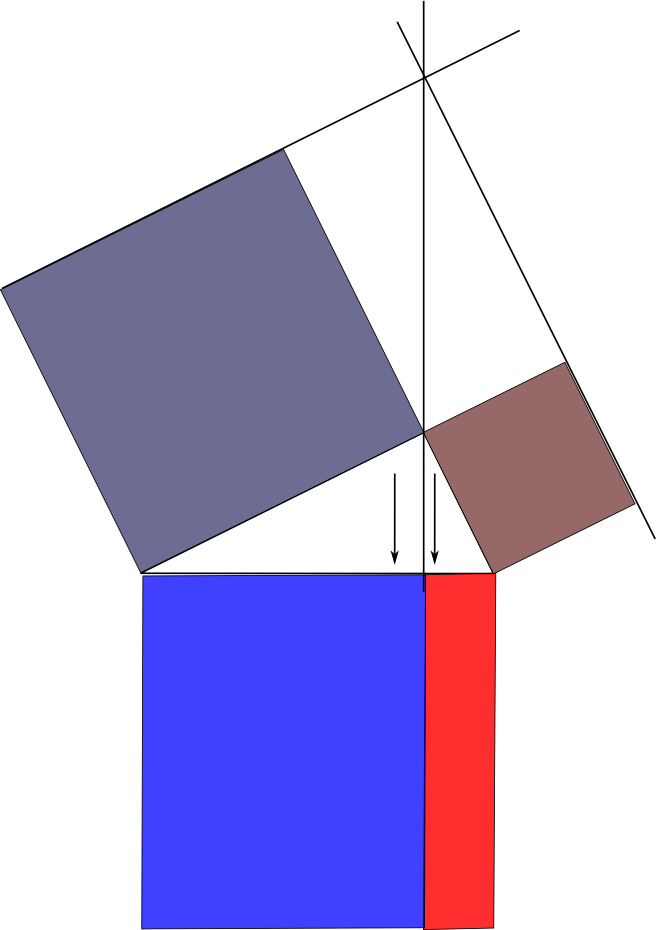
Scherung III

Kathetensatz
Dieser Beweis des Satzes von Pythagoras zeigt außerdem die Gleichheit von `a^2` mit `p*c` und `b^2` mit `q*c`, ist also zugleich ein Beweis für den Kathetensatz.


Beweis über eine andere Ergänzung
Der folgende Beweis nutzt die gleiche Methode, wie sie bei der Einführung der irrationalen Zahlen mit Hilfe der Gelmerbahn verwendet werden kann. In untenstehender Grafik sieht man, dass der Flächeninhalt des Gesamtquadrates c² beträgt. Die Inhalte der einzelnen Teilfiguren addieren sich zu 2 ab + (b-a)²:
`c^2 = 4 * 1/2 a*b + (b-a)^2`
`c^2 = 2 ab + b^2 - 2ab + a^2`
`c^2 = b^2 + a^2`



Pythagoras über Ergänzung