Funktion mit waagerechter Tangente, die nicht TIP, HOP oder TEP ist
| Vorbemerkung |
| Definition der Funktion |
-
`f(x) = x^2*sin(1/x)` für `x != 0` und
`f(x) = 0` für `x = 0` - Diese Funktion ist stetig in 0, da `lim_(x->0)f(x) le lim_(x->0)|x^2*1| = 0`. Denn `-1 le sin(1/x) le +1`
- zur Ableitung:
`f'(x) = 2x*sin(1/x) + x^2*cos(1/x)*(-1/x^2) = 2x*sin(1/x)-cos(1/x)` -
Die Ableitung lässt sich in `x_0=0` fortsetzen, wenn man den Differentialquotient bildet:
`lim_(h->0)(f(x+h)-f(x))/h = lim_(h->0)(f(0+h)-f(0))/h = lim_(h->0)f(h)/h = lim_(h->0)(h^2*sin(1/h))/h = lim_(h->0)h*sin(1/h) = 0,
da `h->0` und `sin(1/h) in [-1;+1]` - Da die Funktion aber umso stärker oszilliert, je näher sie der Null kommt, lässt sich keine Aussage über den Wert der Ableitung in der unmittelbaren Umgebung von Null machen.
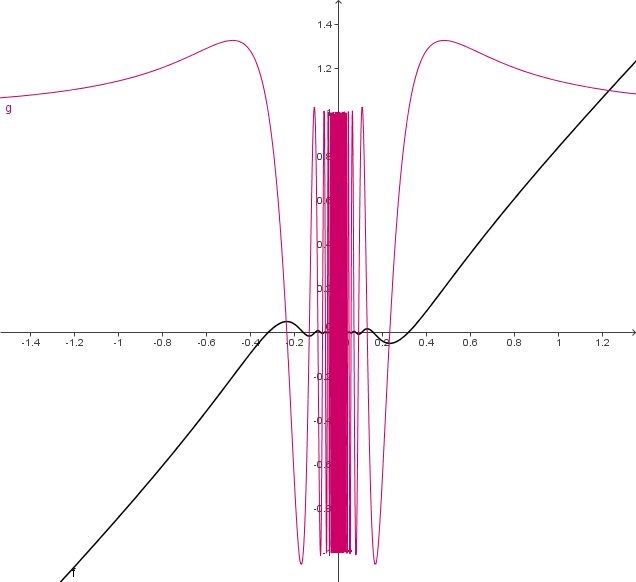
x^2sin(1/x)