UHU-Startseite►Mathematik►Jahrgangsstufen►10►Exponentielles Wachstum und Logarithmen►Beispiele für exp. Anstieg und Abnahme , Abgrenzung von linearem Wachstum►
Bierschaumzerfall



Glas mit Bierschaum

Zerfall von Bierschaum nach dem Einschenken
Ein Glas Bier wird eingeschenkt und die Höhe des Bierschaums wird alle 20s gemessen:
t in s 0 20 40 60 80 100 120 140 160 180 200
h in cm 8,0 6,5 5,5 4,0 3,5 3,0 2,5 2,0 1,7 1,4 1,3




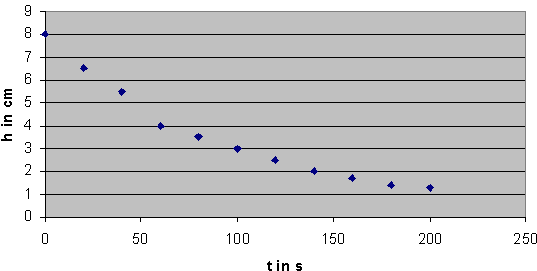
Diagramm: Bierschaumzerfall

Frage: Gibt es eine mathematische Funktionsvorschrift für ein derartiges Verhalten?


Änderungsverhalten
  1. Nimmt der Schaum im Zeitintervall jeweils um die gleiche Menge ab (Subtraktion einer bestimmten Zahl)?
  2. Durch Differenzenbildung lässt sich der neue Wert nicht finden
  3. Der Quotient aus Wert und Vorgängerwert schaut interessanter aus:



Quotiententabelle
Für eine einheitliche mathematische Darstellung werden
  1. die Messvorgänge durchnummeriert
  2. Höhen nur als Prozentsatz der ursprünglichen Höhe angegeben
Messnr. 0   1   2   3   4   5   6   7   8   9   10
Schaumhöhe 100%   81%   69%   50%   44%   38%   31%   25%   21%   18%   16%
Quotient 0,81 0,85 0,73 0,88 0,86 0,83 0,80 0,85 0,82 0,93
Arithmetisches Mittel der Quotienten: 0,84
*Weißbier 2008: die ersten acht Messwerte haben eine Basis von 0.82, die weiteren eher eine Basis > 0.9


Bestimmung des Funktionsterms
  1. Der erste Funktionswert ist 100% = 1
  2. Um zum nächsten Funktionswert zu gelangen muss man mit ≈0,83 multiplizieren
Berechnete Tabelle
x 0 1 2 3 4 5 6 7 8 9 10
y 1,00 0,83 0,69 0,57 0,47 0,39 0,33 0,27 0,23 0,19 0,16
Die dargestellte Tabelle entspricht der Funktion:

`f(x) = 0.83^x`   mit   `D_(f )= NN`

Zurückrechnung auf die Zeichnung (Multiplikation der berechneten Funktionswerte mit 8,0cm)



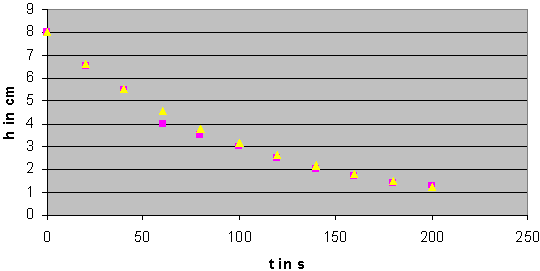
Berechneter Bierschaumzerfall im Vergleich zur Messung


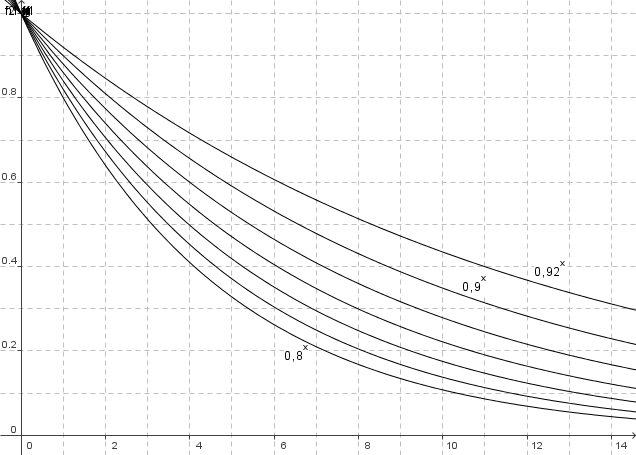
Referenz: Bierschaumzerfall mit verschiedenen Basen
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion