Erweiterung auf die reellen Zahlen: möglicher Weg


Über Zahlbereichserweiterungen
  • Anknüpfen und Motivation (B5:Thermometer)
  • Symbolische Darstellung der neuen Zahlen, Einbettung, Anordnung im bestehenden Zahlensystem
  • Plausible Regeln aufstellen: Operatoren auf die neuen Zahlen anwenden
  • Permanenzprinzip: Gelten die Rechengesetze mit diesen Regeln noch?
  • Gelten auch andere Methoden noch mit den "neuen Zahlen"? (B. Äquivalenzumformungen, Multiplikation von Ungleichungen in ℕ und ℤ )



Vorgehen im einzelnen
  1. Motivation der Gleichung `x^2 = 2`
  2. Zeigen, dass die Gleichung keine Lösung in `QQ` hat
  3. Definition der irrationalen Zahlen, Darstellung durch √
  4. Existenz der irrationalen Zahlen auf der Zahlengeraden
  5. Annäherung der Zahlen über Intervallschachtelung oder Heronverfahren
  6. Rechnen mit irrationalen Zahlen
  7. Vorsicht bei Anwendung des Radizierens als Äquivalenzumformung



Motivation
z.B. über das Seitenverhältnis Din-genormter Blätter oder die Diagonalenlänge eines Quadrates.


Symbolische Darstellung
Über die Wurzeldarstellung z.B. `sqrt 5`


Nachweis, dass `sqrt 2` nicht rational ist (PFZ)
  • Quadratzahlen sind von der Form `(a^n*b^m...)*(a^n*b^m*...) = a^(2n)*b^(2m)*...`
  • Quadratzahlen haben also geradzahlige Exponenten
  • Ausgehend von der Gleichung `a^2 = 2 b^2` stellt man fest: `b^2` ist Quadratzahl, also kommt 2 in der PFZ von `b^2` mit einem geraden Exponenten vor
  • dann wird 2 in `a^2` aber mit einem ungeradzahligen Exponenten auftauchen
  • WIDERSPRUCH!



Nachweis, dass `sqrt 2` nicht rational ist (nach Euklid)
Annahme `sqrt 2` ist eine rationale Zahl, also als vollständig gekürzter Bruch darstellbar.
`sqrt 2 = p/q`
`=> p/q*p/q = p^2/q^2 = 2` oder `p^2 = 2*q^2`
`=> p^2` ist durch 2 teilbar.
Die Primfaktoren von p und q kommen in `p^2` und `q^2` alle doppelt vor
Wenn also 2 als Faktor in p enthalten ist, dann muss `2*2` in `p^2` enthalten sein
Nach `p^2 = 2*q^2` muss die zweite 2 also in `q^2` enthalten sein
`=> q^2` enthält auch `2*2`
`2 | p` und `2 | q => p/q` lässt sich kürzen
Widerspruch zur Annahme.



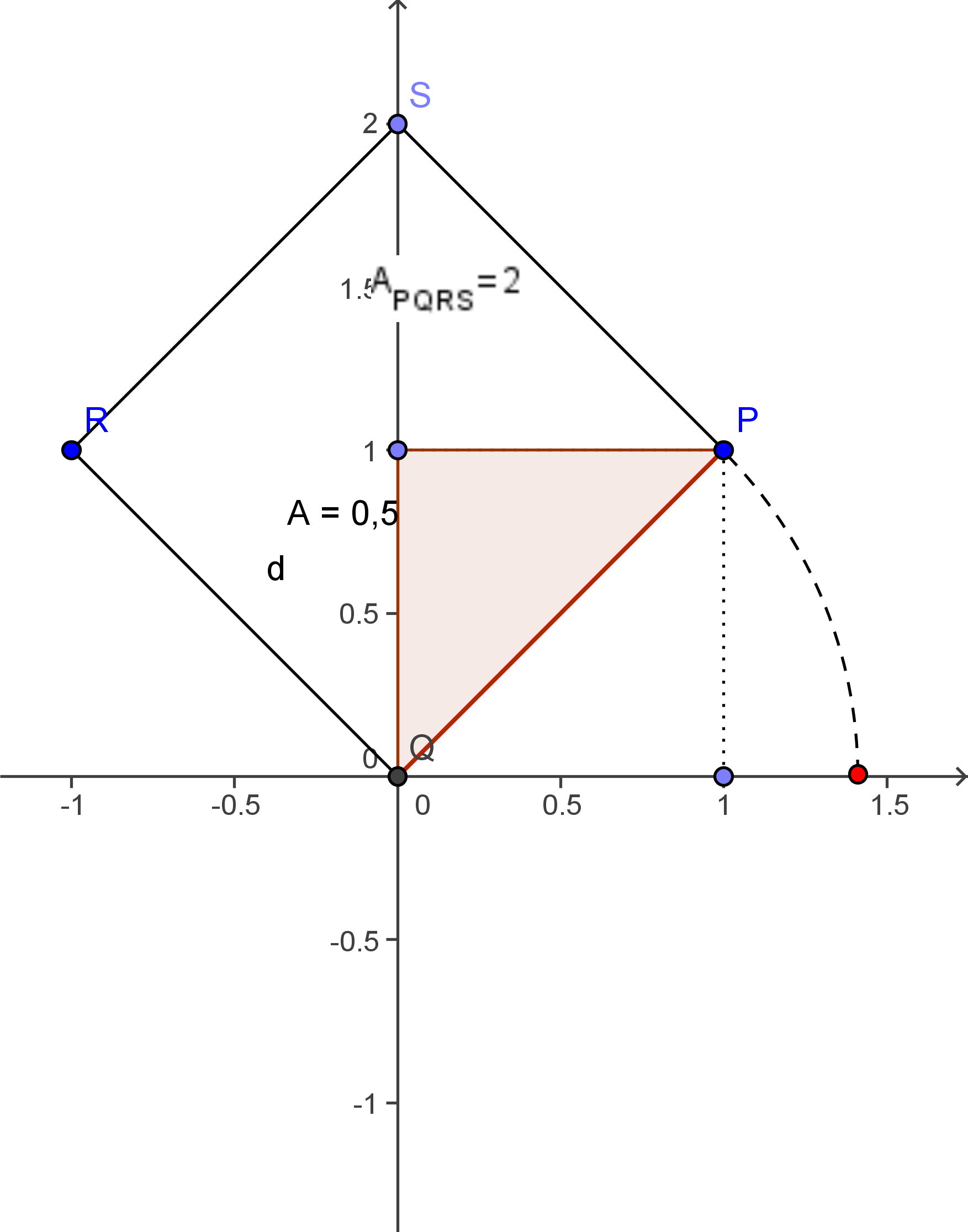
Wurzel 2 auf der Zahlengerade

Dezimalbruchdarstellung von irrationalen Zahlen
Hier eignet sich gut das Heronverfahren in einem Tabellenkalkulationssystem (am NTG werden zur gleichen Zeit Tabellenkalkulationssysteme in Inf besprochen).


Rechnen mit Wurzeln
Vertauschbarkeit des Radizierens mit Multiplikation und Division. Es ist darauf zu achten, dass der Umgang mit Wurzeltermen genug geübt ist.
Die Schüler sind es nicht gewöhnt mit formalen Gesetzen zu arbeiten.


Äquivalenzumformungen mit Radizieren
Beachtung, dass das Radizieren beider Seiten zu zwei verschiedenen Gleichungen führen kann:
`x^2 = 4`
`x = +- 2` für `x in RR`


Beispiel: Beweis, dass 3 = 4 ist
`3 = 4`
`a = b`
`2a = 2b`
`2a - 7 = 2b - 7`
`(2a - 7)^2 = (2b - 7)^2`
`4a^2 - 28 a + 49 = 4b^2 - 28b + 49`
`4a^2 - 28a = 4b^2 - 28b`
`4*9 - 28*3 = 4*16 - 28*4`
`36 - 84 = 64 - 112`
`-48 = -48`
also 3 = 4


Hier die gesamte Vorgehensweise nochmals in Kurzform.