Aufgaben
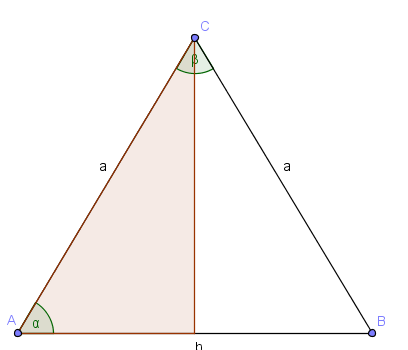
Gleichschenkliges Dreieck
| Gleichschenkliges Dreieck | nach "geometrie 10. schuljahr":Kratz, Schweiger, Wörle |
Berechne a, b, `alpha`, `beta` mit drei gültigen Ziffern bzw. auf Zehntel Grad, wenn folgende Stücke gegeben sind:
- `a = 20.0 cm; b = 12.1 cm`
- `b=48.3 cm; h_a = 41.0 cm`
- `alpha = 37.0°; a = 15.0cm`
- `A=120cm^2; h_a=6.0cm`
| Lösungen |
- `cos alpha = b/(2a) => alpha = 72.4° => beta = 180° - 2 alpha = 35.2°`
- `sin alpha = h_a/b = 0.85 => alpha = 58.1°`
- `beta = 180° - 2 alpha = 106°; b/(2a) = cos alpha => b = 2a*cos alpha = 30.0cm * cos(37°) = 24.0cm`
- `A = 1/2*g*h = 1/2*a*h_a => a = 2*A/h_a = (240cm^2)/6.0cm = 40cm; `