Quadratische Funktionen

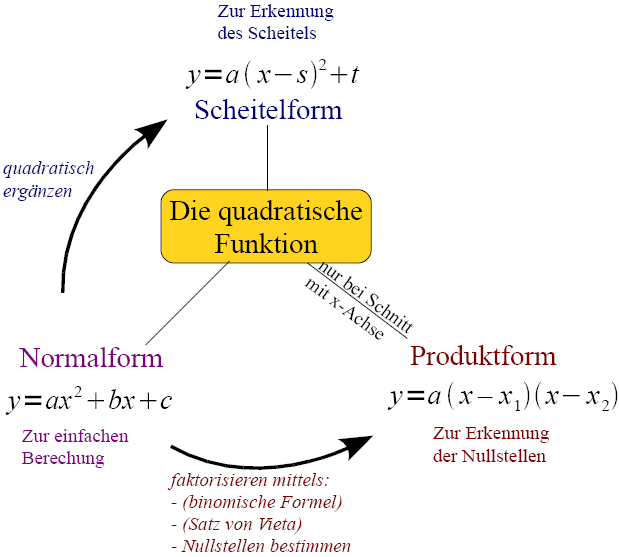
Übersicht: Termarten quadratischer Funktionen

Scheitelpunktsform

`f(x) = a (x + s)^2 + t`

a	Streckung/Spiegelung in y-Richtung
	\|a\| < 1: Stauchung in y-Richtung
	\|a\| > 1: Streckung in y-Richtung
	a < 0: Spiegelung an der x-Achse
s	Verschiebung nach links
	s < 0: Verschiebung nach rechts
	s > 0: Verschiebung nach links
t	Verschiebung nach oben
	s < 0: Verschiebung nach unten
	s > 0: Verschiebung nach oben

Allgemeine Form

`f(x) = a x^2 + b x + c` mit `a, b, c in RR`

Scheitelform → allgemeine Form

`2*(x+3)^2 - 11 = 2*(x^2 + 6x + 9) - 11 = 2x^2 +12 x + 18 - 11 = 2x^2 + 12x + 7`
ausmultiplizieren des quadratischen Terms

Allgemeine Form → Scheitelpunktsform

`-3 x^2 + 12 x - 3`
`-3*(x^2 - 4 x + 1)` (a ausklammern)
`-3*(x^2 - 4 x + 2^2 - 2^2 + 1)` (quadratisch ergänzen)
`-3*((x - 2)^2 - 2^2 + 1)` (binomisch zusammenfassen)
`-3*((x - 2)^2 - 3)` (Konstante zusammenfassen)
`-3*(x - 2)^2 + 9` (äußere Klammer auflösen)
Ergebnis: Spiegelung nach unten, Streckung um Faktor drei, Verschiebung um 2 nach rechts und 9 nach oben