Umkehrfunktionen
`2 |-> 8`
`3 |-> 27`
`1/2 |-> 1/8`
oder als Funktion:
`f: x |-> x^3`
Welche Seitenlänge hat ein Würfel des Volumens 4?
Gesucht ist die Umkehrfunktion der kubischen Funktion:
`8 |-> 2`
`27 |-> 3`
oder als Funktion:
`f^(-1)(x) = root 3 x = x^(1/3)`
insgesamt:
`x_0 stackrel"f"(|->) y_0 stackrel"f^(-1)"(|->) x_0`
| Rechnerische Bestimmung der Umkehrfunktion |
Aus y soll wieder x bestimmt werden. Also für y was einsetzen und x berechnen.
Das ist ungewohnt. Also x und y vertauschen:
`x = y^3` und nach y auflösen
`x^(1/3) = (y^3)^(1/3)`
`x^(1/3) = y`
`root 3 x = y`
`=> f^(-1)(x) = root 3 x`
Zur Bestimmung der Umkehrfunktion:
- x und y vertauschen
- nach y auflösen
| Grafische Bestimmung der Umkehrfunktion |
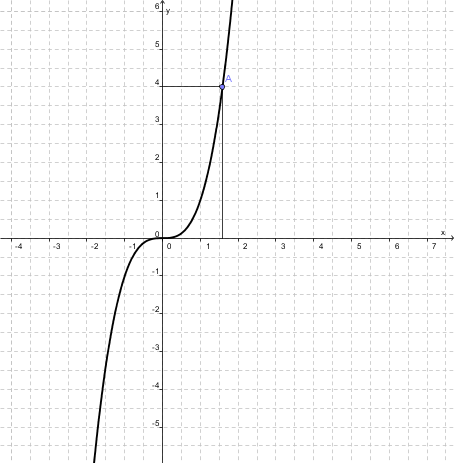
Kubische Funktion mit Würfelvolumen 4

Umkehrfunktion der kubischen Funktion
Zur Bestimmung des Graphen der Umkehrfunktion müssen die Achsen vertauscht, der Graph also an der Winkelhalbierenden des I. Quadranten gespiegelt werden.
| Umkehrbarkeit |
Eine Funktion ist umkehrbar, wenn keine 2 x-Werte zum gleichen Funktionswert führen. Notfalls muss der Definitionsbereich eingeschränkt werden.
Betrachte nur den Ast der Normalparabel, der sich im I. Quadranten befindet. Welche besondere Eigenschaft besitzt er?
Eine Funktion ist den Intervallen umkehrbar, in denen sie streng monoton steigt.