Lösung dazu
- Die Hoch- und Tiefpunkte von f(x) sind die Nullstellen von f'(x), also besitzt f'(x) Nullstellen bei `x_text(1/2) = +-1`. Am steilsten ist der Graph von f bei x=0, hier muss f'(x) einen Tiefpunkt haben.
- Nachdem f(x) punktsymmetrisch erscheint, wird f'(x) achsensymmetrisch sein
- f'(0) = -2 (Tangente einzeichnen, Steigungsdreieck ablesen) und f'(-1,5) = 2,5
- siehe unten
- `int_1^2 f'(x) dx = f(2)-f(1) = 2.8 - 0 = 2.8`
- `int_(-1)^1 f'(x) dx = f(1)-f'(1) ~~ 0 - 2.8 = -2.8`
Der Graph der Ableitungsfunktion schließt etwa einen Flächeninhalt von 2.8 mit der x-Achse ein
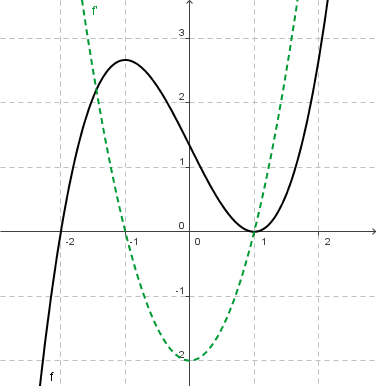
Graph der Ableitungsfunktion