UHU-Startseite►Mathematik►Jahrgangsstufen►12►Flächeninhalt und bestimmtes Integral►Berechnung von Flächeninhalten►
mit ganzrationalen Funktionen (Lsg)


1.
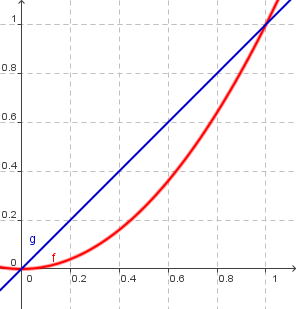
Die beiden Graphen treffen sich in (0|0) und (1|1), dabei verläuft `f(x) = x^2` unterhalb von `g(x) = x`, denn eine Zahl kleiner 1 wird bei Multiplikation mit sich selbst noch kleiner:



Flächen zwischen f(x)=x² und g(x)=x

`f(x) = g(x) => g(x) - f(x) = 0 => x - x^2 = x*(1-x) = 0 => x_1 = 0; x_2 = 1`

`int_0^1 x - x^2 dx = [x^2/2 - x^3/3]_0^1 = 1/2 - 1/3 - 0 = 1/6`

Der Flächeninhalt zwischen den Graphen beträgt `1/6`


2
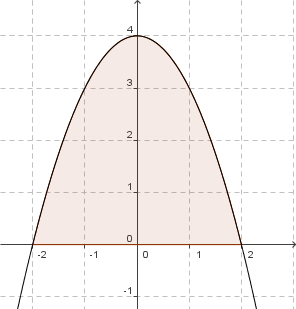
Der Graph ist eine Normalparabel die nach unten geöffnet und um 4 nach oben verschoben ist:



4-x² mit Flächeninhalt

Nullstellen:

`4 - x^2 = 0 => (2-x)(2+x) = 0 => x_text(1/2) = +- 2`
Flächeninhalt:

`int_(-2)^2 4 - x^2 dx = [4x - x^3/3]_(-2)^2 = 8 - 8/3 - (-8 + 8/3) = 2*(8-8/3) = 2*16/3 = 32/3`
Der Flächeninhalt beträgt `32/3 = 10 2/3`


3.
Der Graph der `x^3`-Funktion wurde linear transformiert:
  • An der y-Achse gespiegelt
  • und um 1 nach oben verschoben
Damit verläuft er so:



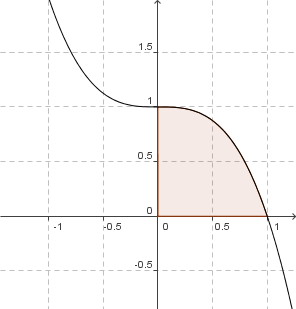
1-x³

Schnittpunkte mit den Achsen:

`f(0) = 1 - 0^3 = 1 => S_Y(0|1)`

`f(x) = 0 = 1 - x^3 => x^3 = 1 => x = 1 => S_X(1|0)`

Also wird folgendermaßen integriert:

`int_0^1 1 - x^3 dx = [x - x^4/4]_0^1 = 1 - 1/4 - 0 = 3/4`

Der Flächeninhalt beträgt `3/4`.


4.
Bestimmung der Funktionsgleichung der Tangente `f(1) = 1^3 = 1 =>` P(1|1) ist Tangentenpunkt

`f'(x) = 3 x^2` und `f'(1) = 3`

`m_T = 3` gesucht ist noch `t_T`

`T(x) = 3 x + t_T`

Tangente geht auch durch P:

`1 = 3*1 + t_T => t_T = -2`

Tangentengleichung: `T(x) = 3x - 2`
Schnittpunkte der beiden Graphen:

`T(x) = f(x) => 3x - 2 = x^3 => x^3 - 3x + 2 = 0`

Bekannt ist bereits die Nullstelle `x=1`, weil sich die Graphen hier berühren. Gesucht wird die 2. Nullstelle. Dazu muss eine Polynomdivision durchgeführt werden, es ergibt sich

`x^3 - 3x + 2 = (x-1)*(x^2+x-2)`

also `x^2+x-2 = (x-1)(x+2) => x_2=-2` ist zweite Nullstelle.

Die Graphen treffen sich also ein zweites mal bei (-2|-8)

Gesamte Fläche

`int_(-2)^1 x^3 - 3x + 2 dx = [x^4/4 - 3/2 x^2 + 2x]_(-2)^1 = 6 3/4`

Zwischen dem Graph und der Tangente wird also ein Flächeninhalt von `6 3/4` aufgespannt.



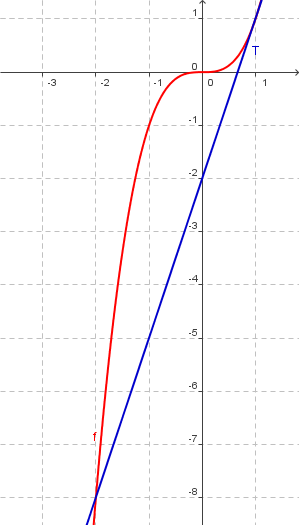
x³ mit Tangente
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion