UHU-Startseite►Mathematik►Jahrgangsstufen►12►Flächeninhalt und bestimmtes Integral►Berechnung von Flächeninhalten►
mit der Exponentialfunktion (Lsg)


1
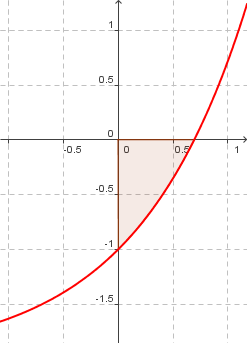
Der Graph verläuft zu einem Teil durch den IV. Quadranten und schließt dort mit x- und y- Achse einen Flächeninhalt ein:



Graph von exp(x)-2 im IV. Quadranten

Schnittstellen mit den Achsen:

`f(0) = -2 => S_Y(0|-2)`
`f(x) = 0 = e^x - 2 => x = ln(2) => S_X(ln(2)|0)`

Berechnung des Flächeninhaltes:

`int_0^(ln(2)) e^x-2 dx = [e^x - 2x]_0^(ln(2)) = e^(ln(2)) - 2*ln(2) - (1-0)`

`= 2 - 2*ln(2) - 1= 1 - 2*ln(2) = -0.39`

Es ergibt sich ein Flächeninhalt von 0.39.


2
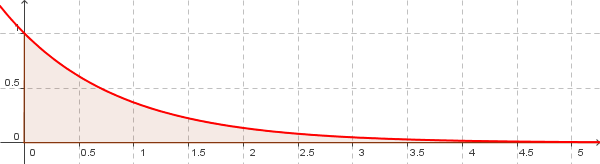
Die Fläche liegt im gesamten 1. Quadranten und zieht sich dort bis ins Unendliche. Interessant also, ob der Flächeninhalt endlich ist.



exp(-x) und x-Achse im I.Quadranten

`lim_(x->oo) int_0^x e^(-t) dt = lim_(x->oo) [-e^(-t)]_0^x`

`= lim_(x->oo) (-e^(-x) + 1) = 1`


3
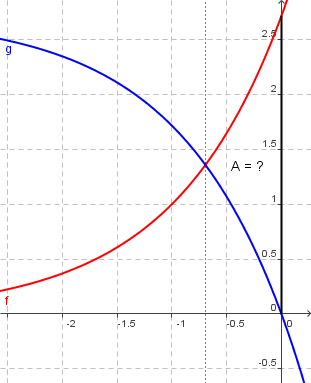
Die Fläche erstreckt sich zwischen dem Schnittpunkt der zwei Graphen im II. Quadranten, den zwei Graphen und der y-Achse:



Darstellung der Graphen und des Flächeninhaltes

Schnittpunkt der Graphen:

`f(x) = g(x) => f(x) - g(x) = 0`

`e^(x+1) - (e - e^(x+1)) = 0`

`2*e^(x+1) - e = 0`

`2*e^(x+1) = e` | ln()

`ln(2*e^(x+1) = ln (e^1)`

`ln(2) + ln(e^(x+1)) = 1`

`ln(2) + x + 1 = 1`

`ln(2) + x = 0 => x = - ln(2)`

Flächeninhalt zwischen den Graphen im Intervall von -ln(2) bis 0:

`int_(-ln(2))^0 2*e^(x+1) - e dx = [2*e^(x+1) - e*x]_(-ln(2))^0`

`= 0.83`

optimal sichtbar mit Firefox Formeln mit asciimath Druckversion