|
Rückwärts aufgezogen
Bestimme alle Nullstellen der Funktion:
`f(x) = 4 x^4 - 4 x^3 + x^2 - 4 x - 3`
Wie viele können es höchstens sein?
| Eine Zauberformel zur Annäherung an Nullstellen |
`x_(n+1) = x_n-f(x)/(f'(x))`
- Starte mit irgendeinem x und wende diese Formel so lange an, bis sich die entstandene Zahl nicht mehr ändert. Die entstandene Zahl ist eine Nullstelle von `f(x)`!
-
Starte zur Suche weiterer Nullstellen mit anderen Startwerten. Wie viele verschiedene Nullstellen erhältst Du?
xn f(xn) f'(xn) xn-f(xn)/f'(xn)
0 -3 -4 -0.75
-0.75 3.52 -19 -0.56
-0.56 0.71 -11.85 -0.51
-0.51 0.05 -10.14 -0.5
-0.5 0 -10 -0.5
-0.5 0 -10 -0.5
xn f(xn) f'(xn) xn-f(xn)/f'(xn)
4 765 836 3.08
3.08 239.02 357.71 2.42
2.42 73.16 156.59 1.95
1.95 21.14 72.84 1.66
1.66 5.16 39.37 1.53
1.53 0.76 28.13 1.5
1.5 0.03 26.08 1.5
1.5 0 26 1.5
xn f(xn) f'(xn) xn-f(xn)/f'(xn)
2 25 80 1.69
1.69 6.31 42.09 1.54
1.54 1.03 28.86 1.5
1.5 0.05 26.14 1.5
1.5 0 26 1.5
- Lege die Tangente an den Graphen, und
- suche deren Nullstelle das ergibt
- den neuen Startwert
| Vor- und Nachteile des Verfahrens |
Vorteile:
- wenn NSt. nicht berechenbar, dann immer noch näherungsweise angebbar
Nachteile:
- Genaue Position der NSt. evtl. nicht angebbar (Beispiel: `sqrt 2`)
- Anzahl der Nullstellen bleibt unbekannt
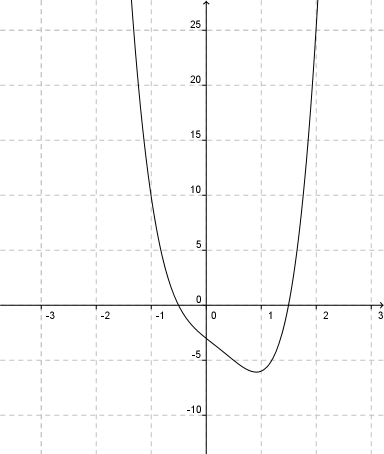
Graph der Funktion mit den gesuchten Nullstellen
| Im Beispiel für Startwert 0 |
`f'(0)=-4; f(0)=-3`
gesucht Achsenabschnitt t der Tangente:
`-3 = -4*0+t => t = -3 - (-4*0) = -3 = f(0) - f'(0)*0 = f(x_n) - f'(x_n)*x_n`
`=> T_1(x) = -4x-3; T_1(x) = 0 => -4 x - 3 = 0 => x = 3/(-4) = -(3/4)`
`x_(n+1) = (-t)/m = -(f(x_n)-f'(x_n)*xn)/f'(x_n) = x_n - f(x_n)/f'(x_n)`
|
