3.3
| 3 |
- Maximaler Definitionsbereich: `x in RR`
-
Symmetrie:
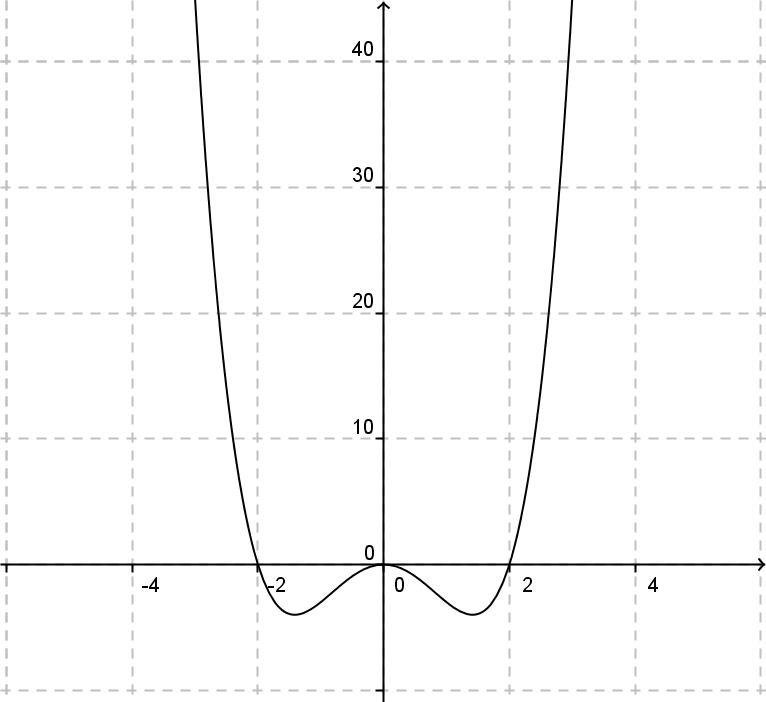
`f(-x) = (-x)^4 - 4 (-x)^2 = x^4 - 4 x^2 = f(x)` (Achsensymmetrie!) - Verhalten im Unendlichen
`lim_(x->+oo) f(x) -> +oo` und wg. Symmetrie auch `lim_(x->-oo) f(x) -> +oo` -
Gemeinsame Punkte mit den Koordinatenachsen
y-Achse: `f(0) = 0 => S_y(0;0)`
x-Achse: `f(x) = 0 = x^2*(x^2-4) => x_1 = -2; x_2 = 0; x_3 = +2` `=> N_1(-2;0); N_2(0;0); N_3(2;0)` - Monotonie
`f'(x) = 4 x^3 - 8 x`; `f'(x) = 0 = 4 x ( x^2 - 2 )`
`x_4 = 0; x_5 = - sqrt 2; x_6 = sqrt 2`
- Krümmungsverhalten
`f''(x) = 12 x^2 - 8`; `f''(x) = 0 => x^2 = 2/3 => x_(7text(/)8) = +- sqrt(2/3)`
-
| 6 |
`B -> f_6`, weil punktsymmetrisch
`C -> f_2`, wg. Nullstellen bei `+-3`
`D -> f_1`, um 4 nach oben verschoben und `1 lt f(1) lt 2`
`E -> f_7`