Fünfeck
| Zeichnen der Figur |
- Nimm Deinen Zirkel und zeichne einen Kreis mit Radius 4cm
- Teile den Kreis vom Mittelpunkt aus in 5 gleichgroße Sektoren mit dem Winkel: `mu = (360°)/5 = 72°`
- Verbinde die Eckpunkte aller Sektoren durch einen geschlossenen Streckenzug
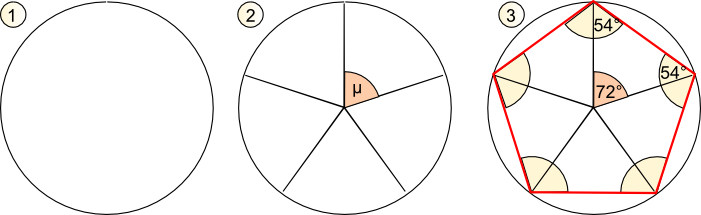
Zeichnung: Regelmäßiges Fünfeck
| Berechnen der Innenwinkelsumme |
- im Teildreieck:
`mu = 72°, alpha = beta`
`alpha + beta = 180°-72`= 108° => alpha = beta = 54°` - Innenwinkelsumme gesamtes Fünfeck:
(Summe aller Winkel der Ecken am Kreis)
Jedes Teildreieck trägt 108° bei:
`S = 5*108° = 540°`
Ein regelmäßiges Fünfeck hat die Innenwinkelsumme 540°