Problembenennung; Streifenmethode exemplarisch


Problemstellung
Frei nach dem Abitur 2011:
Die in `RR` definierte Funktion `h: x|->6*e^(-0.5 x)+1.5` beschreibt modellhaft die Entwicklung des momentanen Schadstoffaustoßes einer Maschine. Dabei ist x die seit dem Start der Maschine vergangene Zeit in Minuten und h(x) die momentane Schadstoffausstoßrate in Milligramm pro Minute.
Wie groß ist die gesamte, nach 5 Minuten ausgestoßene Schadstoffmenge?


WH: Aussagen über den Graphen der Funktion
Es handelt sich um eine lineare Transformation der e-Funktion:
  1. Der Faktor 0,5 bewirkt eine Dehnung des ursprünglichen Graphens mit dem Faktor 2 in x-Richtung
  2. Das negative Vorzeichen bewirkt eine Spiegelung an der y-Achse
  3. Der Faktor 6 bewirkt eine sechsfache Dehnung des Graphens in y-Richtung
  4. Der Summand 1,5 bewirkt eine Verschiebung um 1,5 in y-Richtung (nach oben)




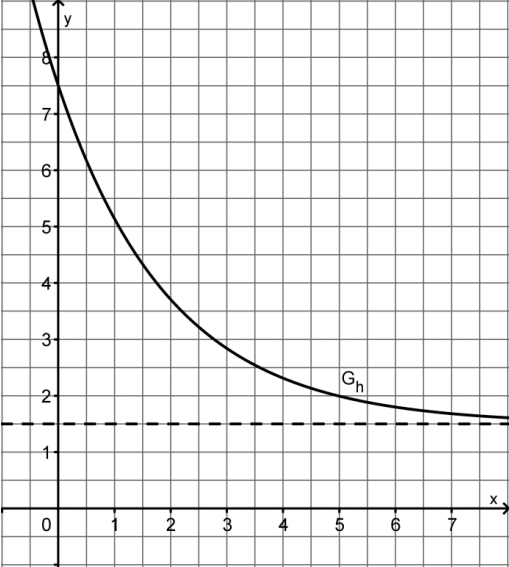
Der Graph der Funktion

Interpretation im Graphen
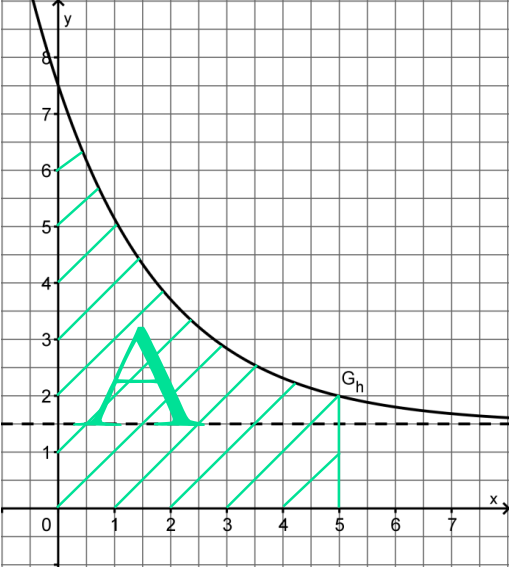
Die gesuchte Größe entspricht dem Flächeninhalt zwischen x-Achse und Graphen im Interval `x in text([)0;5text(])`:



Gesuchter Flächeninhalt

  • Der gesuchte Flächeninhalt lässt sich bisher nur näherungsweise berechnen, z.B. durch
  • Kästchenzählen oder
  • eine geeignete Trapezfläche



Nachteile:
  • Größe des Fehlers nicht bekannt
  • Annäherung nicht systematisch möglich
anderes Verfahren:



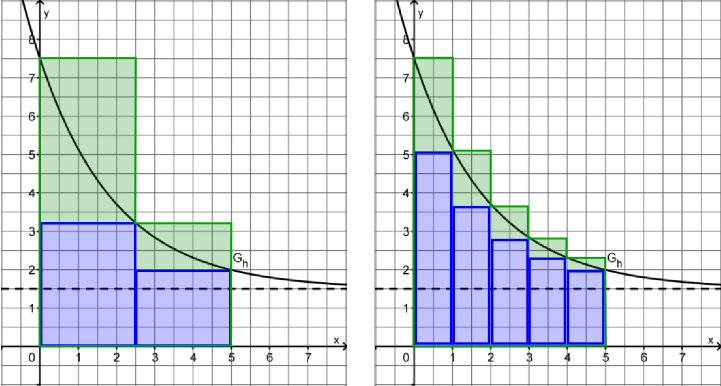
Streifenmethode

Berechnung
Bei zwei Streifen:
Untersumme
`s_2 = 2.5*(3.25+2) = 13.12
Obersumme
`S_2 = 2.5*(7.5+3.25) = 16.88

Bei fünf Streifen:
Untersumme
`s_5 = 1*(5.15+3.71+2.84+2.31+1.99)=15.99`
Obersumme
`S_5 = 1*(7.5+5.15+3.71+2.84+2.31)=21.5`



Streifenmethode
Zur Annäherung des Flächeninhaltes werden vertikale Streifen verwendet:
Die Summe der Inhalte der einbeschriebenen Rechtecke heißt Untersumme, die der umbeschriebenen Rechtecke Obersumme.
Mit größer werdender Streifenzahl nähern sich Unter- und Obersumme dem gesuchten FI an.


Hausaufgabe
  1. Welche Veränderungen müssen am Graph der Funktion `f(x)=sin(x)` vorgenommen werden um den Graph von `-2 sin(x-3) + 1,5` zu erhalten?
    1. Bestimmung von `S_4` und `s_4` für `h(x)`. Schätzen des tatsächlichen Schadstoffaustoßes.
    2. Bestimmung von `S_2`, `s_2` für den Flächeninhalt zwischen dem Graphen von `f(x) = 2-x` und der x-Achse.