|
Planung für "Einführung in die Streifenmethode"
Die Schüler lernen, Integrale zu berechnen und in Sachzusammenhängen anzuwenden. Dazu begründen sie den Hauptsatz der Differential- und Integralrechnung mithilfe anschaulicher Überlegungen und stellen die Verbindung mit der aus Jahrgangsstufe 11 bekannten Stammfunktion her. Sie erkennen, dass Differenzieren und Integrieren Umkehroperationen sind.
- bestimmtes Integral, Integralfunktion
- Hauptsatz der Differential- und Integralrechnung
- Berechnung von Flächeninhalten
| Unterrichtssequenz; Abgrenzung der Stundeninhalte |
Es handelt sich um die erste Stunde zum Thema. Das Buch beginnt mit der Berechnung von Flächeninhalten mit Hilfe der Streifenmethode und kommt im zweiten Kapitel zum HDI. Um Aufgaben aus dem Buch bearbeiten zu können und die Schüler nicht zu weit vom Lehrwerk zu unterrichten, sollte also in dieser Stunde auch die Idee der Flächenberechnung und die Streifenmethode eingeführt werden.
Als Frage bleibt, ob allgemeine Berechnungen noch mit in die Stunde integriert werden sollten oder nicht. Dazu werden beispielsweise die ersten Aufgaben im Buch konsultiert. Hier ist genug Material um vorerst noch keine allgemeinen Formeln zu erarbeiten. Im Vordergrund sollte also die Nachvollziehbarkeit der Streifenmethode als solches liegen und nicht deren formale Darstellung bzw. Verwendung.
- Flächen krummlinig begrenzter Flächen sind im allgemeinen noch nicht berechenbar
- Zur Berechnung sind verschiedene Näherungsverfahren denkbar
- Eine Möglichkeit für eine beliebig genaue Möglichkeit stellt die Streifenmethode dar
- Dazu wird die Unter- und die Obersumme einer vorgegebenen Anzahl von Streifen berechnet
- Eine Erhöhung der Streifenzahl führt zu einer Annäherung von Unter- und Obersumme aneinander und an den tatsächlichen Flächeninhalt
- Zur Veranschaulichung des Grenzwertes bietet sich eine Rechnersimulation an
- Buch: Berechnung des Flächeninhaltes einer von einem Parabelbogen begrenzten Glasfront eines Gebäudes
- Physik: Arbeit im Gravitationsfeld (bei gegebenem r-F-Diagramm
- Berechnung zurückgelegten Entfernung aus der Anzeige von Geschwindigkeit
- Solarzellen: Berechnung der gesamten maximalen Sonnenscheindauer im Sommer mit Hilfe eines Diagramms zu den Tageslängen (Sinusfunktion)
- Abituraufgabe zur Schadstoffaustoßrate
| Festlegung: Modifizierte Abituraufgabe |
Frei nach dem Abitur 2011:
Die in `RR` definierte Funktion `h: x|->6*e^(-0.5 x)+1.5` beschreibt modellhaft die Entwicklung des momentanen Schadstoffaustoßes einer Maschine. Dabei ist x die seit dem Start der Maschine vergangene Zeit in Minuten und h(x) die momentane Schadstoffausstoßrate in Milligramm pro Minute.
Wie groß ist die gesamte, nach 5 Minuten ausgestoßene Schadstoffmenge?
- Darstellen: Graph der Funktion visualisieren und diskutieren
- Modellieren: Gesuchter Schadstoffaustoß entspricht dem Flächeninhalt zwischen Graph und x-Achse bis zur Stelle x = 5
- Problematik der Bestimmung krummlinig begrenzter Flächeninhalte
- Diskussion verschiedener Lösungsansätze
- Ziel: Streifenmethode mit dem Vorteil einer Annäherung mit Fehlerkenntnis
- Anwendung der Streifenmethode für kleine Zahlen und Abschätzung des Flächeninhaltes
Aus Sicht des Schülers ist die gesamte Streifenmethode nur einsehbar, wenn sie grafisch erklärt wird. Deshalb ist es an dieser Stelle unerlässlich den Graphen zu skizzieren. Damit einhergehen können folgende Unterrichtselemente:
- Wiederholung der e-Funktion
- Bestimmung der Funktionswerte h(0) und h(5)
- Bestimmung von h'(x) und h'(0) und h'(5)
- Evtl. Berechnung weiterer Stützpunkte
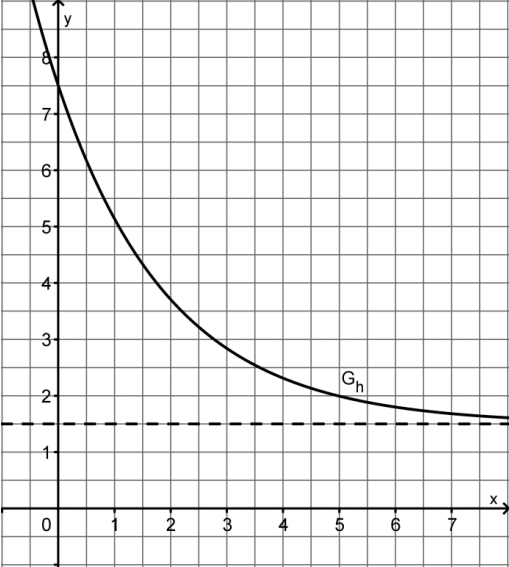
Grafik aus dem Abitur
| Identifikation der gesuchten Größe |
Die gesuchte Größe, also die betrachteten Zeitraum ausgestoßene Schadstoffmenge entspricht im Diagramm der Fläche zwischen Graph und x-Achse bis zur Stelle x=5. Die Maßzahl für den Flächeninhalt entspricht also der Anzahl der in Milligramm freigesetzten Schadstoffmenge.
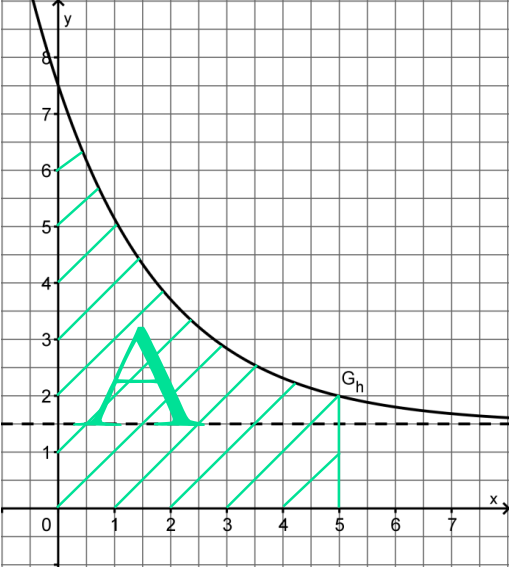
Gesuchter Flächeninhalt
| Diskussion von Abschätzungsvorschlägen |
Insbesondere sollen der Wert von Dreiecken, Trapezen und ähnlichen Figuren als Näherung gelobt werden; alle besitzen aber den Nachteil, dass die Näherung nicht verbessert und der Näherungsfehler nicht berechnet werden kann.
Dies sind Argumente die zur Streifenmethode führen sollen. Hier ist ein Knackpunkt! Wie sollen die Schüler auf die Idee der Streifenmethode kommen?
- Kästchenzählen
- Geometrie einfach halten: Das Rechteck als Grundfigur
- Einfache Teilmöglichkeit vorsehen...
Dieser Stundenteil ist sensibel und hängt stark von der Interaktion zwischen Lehrer und Schülern ab.
| Vorstellung der Streifenmethode |
- Darstellung von `s_2, S_2` mit verschiedenen Farben
- Grobe Definition der Streifenmethode
Zur Annäherung des Flächeninhaltes werden vertikale Streifen verwendet:
Die Summe der Inhalte der einbeschriebenen Rechtecke heißt Untersumme, die der umbeschriebenen Rechtecke Obersumme.
Mit größer werdender Streifenzahl nähern sich Unter- und Obersumme dem gesuchten FI an.
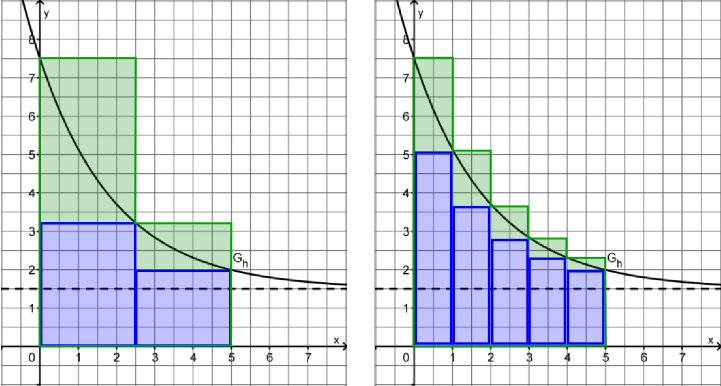
Darstellung von S2 und s2
Austeilen des Graphen auf einem Blatt.
Bestimmung von `s_5, S_5` durch verschiedene Schülergruppen.
Die Schüler
- können das Problem der Bestimmung des Flächeninhalts krummlinig begrenzter Flächen erläutern und veranschaulichen
- können die Streifenmethode anhand eines gegebenen, monoton fallenden Graphen veranschaulichen
- sind in der Lage `S_2, s_2, S_5` und `s_5` bei gegebenem Funktionsterm eines monoton fallenden Graphen zu berechnen
- Welche Veränderungen müssen am Graph der Funktion `f(x)=sin(x)` vorgenommen werden um den Graph von `-2 sin(x-3) + 1,5` zu erhalten?
-
- Bestimmung von `S_4` und `s_4` für `h(x)`. Schätzen des tatsächlichen Schadstoffaustoßes.
- Bestimmung von `S_2`, `s_2` für den Flächeninhalt zwischen dem Graphen von `f(x) = 2-x` und der x-Achse.
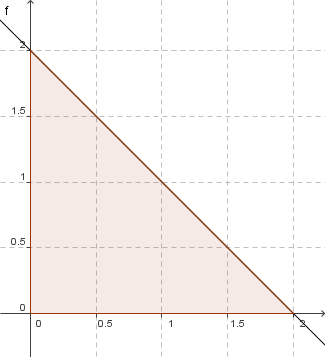
Fläche zwischen dem Graph von 2-x und der x-Achse
In der Folgestunde:
- Erhöhung der Streifenzahl und Annäherung an den gesuchten Flächeninhalt
- Einführung der Definition des bestimmten Integrals
Schülerzentrierte Phase zur Berechnung von `s_5` und `S_5`.
Evtl. geogebra über Beamer zur Veranschaulichung der Streifenmethode für große n
| Phase | Verlauf | Sozialform | Medium |
|---|
| Einführung | --
Übersicht 12. Jgst. | LSG | -- |
| Motivation | Abituraufgabe
Abiaufgabe wird vorgestellt | LSG | OHP |
| Diskussion der Funktion | Erarbeitung versch. Elemente des gesuchten Graphens | LSG,
LSG | Tafel,AB,OHP |
| Problemstellung | Erkennen der gesuchten Größe im Graph; Fixierung des Stundenthemas | LSG | OHP, Tafel |
|



