Die nat. Exponentialfunktion


Zusammenfassung der Voraussetzungen
`f_a(x) = a^x` (allgemeine Exponentialfunktion)
`f_a'(x) = a^x * lim_(h->0)(a^x-1)/h`

und
`lim_(h->0)(a^x-1)/h` existiert für alle `a!=1`
geht gegen 1, wenn `a ~~ 2.7`



Deutung
  • Aus der Existenz des Grenzwertes folgt:
    Die Steigung des Graphen ist in jedem Punkt proprotional zum Funktionswert.
  • `lim_(h->0)(2.7^h-1)/h~~1`. Also `f_(2.7)'(x)~~f_2.7(x)`
    Es gibt eine Basis, für die Funktion und Ableitungsfunktion identisch sind.




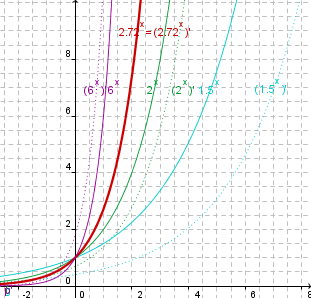
Verschiedene Exponentialfunktionen mit Ableitung

Die Zahl e
Die Basis derjenigen Exponentialfunktion deren Ableitung mit ihr identisch ist wird e (Eulersche Zahl) genannt. Es gilt also:

`(e^x)' = e^x`


Wie groß ist e?
für kleine h gilt: `(e^h-1)/h~~1 => e^h-1~~h => e ~~ (h+1)^(1/h)`

Je kleiner man h wählt, desto exakter wird die Annäherung. Zur besseren Vorstellung kann man `h` auch mit `1/n` substituieren:
`e = lim_(n->oo)(1+1/n)^n`




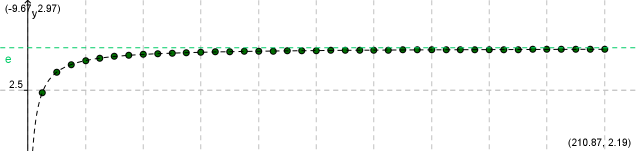
Folge für die Zahl e