Ableitung der allg. Exponentialfkt.


Aktivität
In radioaktiv verstrahlten Gebieten wird der Zugang erst erlaubt, wenn die Aktivität des radioaktiven Materials einen bestimmten Wert unterschreitet.
  • Der Zerfall radioaktiven Materials erfolgt typischerweise exponentiell. Bei einer Halbwertszeit eines bestimmten Cäsiumisotops von 30 Jahren gilt z.B.:
    `f(x) = m_0*2^(-x/30)`, wenn `m_0` die Anfangsmasse und `x` die Zeit in Jahren ist.
  • Da die Aktivität der momentanen Zerfallsrate entspricht ist also die Ableitung dieser Exponentialfunktion gesucht um Vorhersagen für das verseuchte Gebiet machen zu können.



Auf der Suche nach der Ableitung der allgemeinen Exponentialfunktion
Die allgemeine Exponentialfunktion kann durch folgenden Term beschrieben werden:

`f_a(x) = a^x` mit `a!=1` und `x in RR`.

Da keine Ableitungsregel für diesen Term bekannt ist muss mit der h-Methode angesetzt werden:

`f_a'(x) = lim_(h->0) (f(x+h)-f(x))/h = lim_(h->0) (a^(x+h)-a^x)/h = lim_(h->0) (a^x*a^h-a^x)/h = a^x*lim_(h->0) (a^h-1)/h`

Der entstandene Term ist ein Produkt aus der ursprünglichen Funktion `a^x` und einem Grenzwert.
Bei der Untersuchung des Differentialquotienten zu `a^x` stößt man auf den Term:
`lim_(h->0) (a^h-1)/h`



Aussagen über diesen Grenzwert
  1. Numerische Untersuchung:
          h	0,10000	0,01000	0,00100	0,00010	0,00001
a
1,5	0,41380	0,40629	0,40555	0,40547	0,40547
2,0	0,71773	0,69556	0,69339	0,69317	0,69315
2,5	0,95958	0,92050	0,91671	0,91633	0,91629
3,0	1,16123	1,10467	1,09922	1,09867	1,09862
3,5	1,33462	1,26064	1,25355	1,25284	1,25277
4,0	1,48698	1,39595	1,38726	1,38639	1,38630
  2. Der Grenzwert existiert zumindest für die dargestellten a.
  3. Auffallend ist weiterhin, dass der Grenzwert zwischen 2,5 und 3,0 sogar gegen 1 gehen könnte.
  4. Der Grenzwert lässt sich graphisch auch als Differentialquotient deuten:
    Er stellt die Tangentensteigung der Funktion `a^x` im Nullpunkt dar, somit ist seine Existenz plausibel gemacht und die obige Tabelle lässt sich grafisch darstellen:




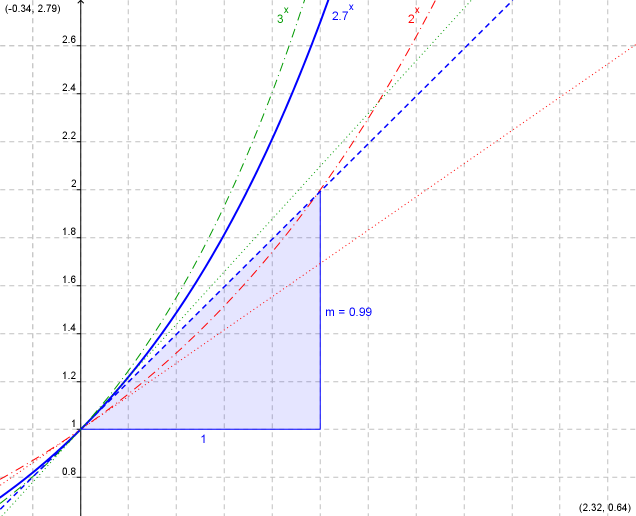
Tangentensteigung bei x=0 für verschiedene Basen

Der Grenzwert `lim_(h->0) (a^h-1)/h`

existiert
und ist für `a ~~ 2.7` ungefähr 1