Der WS-Begriff
| Voraussetzungen |
- `Omega={omega_1, omega_2, ... omega_i}`: Menge aller Ergebnisse
- `A, B in bbb P(Omega)`: Ereignisse aus der Menge aller Teilmengen von `Omega`
- `h_n(A)`: die relative Häufigkeit des Auftretens von A
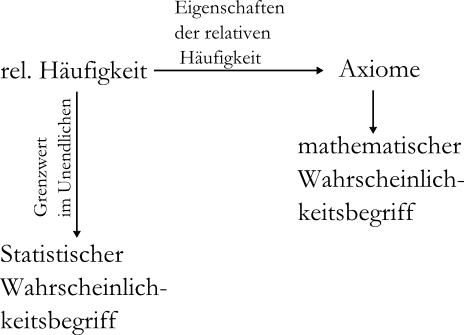
| Eigenschaften relative Häufigkeit |
`h_n(Omega) = 1`
`h_n(O/)= 0`
| Weitere Eigenschaften |
`h_n(A uu B) = h_n(A)+h_n(B)-h_n(A nn B) text( sonst )`
| Definition über Grenzwert |
- Definition nach von Mises:
- `P(A):=lim_(n->oo)h_n(A)`
- hat sich nicht durchgesetzt, da der Limesbegriff sich nicht auf statistische Folgen anwenden lässt.
(Es gibt eben keine Zahl n, ab der alle weiteren relativen Häufigkeiten sich um weniger als `epsilon` von der WS des Ereignisses unterscheiden.)
| Axiome von Kolmogorow |
Eine Funktion `P:A|->P(A)` mit `A in bbb P(Omega)` und `P(A) in RR` heißt Wahrscheinlichkeitsverteilung, wenn sie folgenden Bedingungen genügt:
- Axiom I: `P(A) >= 0` (Nichtnegativität)
- Axiom II: `P(Omega) = 1` (Normierung)
- Axiom III: `A nn B = O/ => P(A uu B) = P(A) + P(B)` (Additivität)