Sinussatz über Mathematik im Gelände
Sinussatz im Gelände
- Spanne eine Schnur in ca. 1m Höhe. Markiere darauf zwei Punkte A und B so, dass ein Punkt C des Nachbargebäudes von diesen beiden Punkten aus sichtbar ist.
ODER
Markiere zwei Punkte auf dem Boden. - Miss die Länge der Strecke [AB].
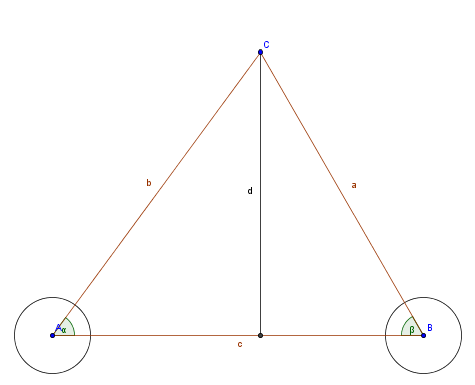
- Bestimme mit der Winkelscheibe die Winkelmaße `alpha` und `beta`.
- Berechne nun die Entfernung `bar (AC)` oder `bar (BC)` und daraus den Abstand des Punktes C von der Strecke [AB].
| Herleitung des Sinussatzes aus der Situation |
Auflösen nach d:
`d = b*sin(alpha); d = a*sin(beta);`
Gleichsetzen:
`b*sin(alpha) = d = a*sin(beta); `
so umstellen, dass korrepondierende Größen beisammen stehen:
`(sin(alpha))/a = (sin(beta))/b`
Hätte man das Lot von A auf a betrachtet, dann wäre herausgekommen:
`(sin(beta))/b = (sin(gamma))/c`
Also gilt:
`(sin(alpha))/a = (sin(beta))/b = (sin(gamma))/c` (Sinussatz)
| Bestimmung der Entfernung von C |
Bestimme b mit Hilfe des Sinussatzes:
`(sin(gamma))/c = (sin(alpha))/a => a = c * (sin(alpha))/(sin(gamma)) = 6m * (0,966)/(0,574) approx 10,1m`
`sin(alpha) = d/a => d = a*sin(alpha) approx 10,1m * 0,966 = 9,76m`