UHU-Startseite►Mathematik►Jahrgangsstufen►12►Geraden und Ebenen im Raum►Geraden►
Beispiel 1



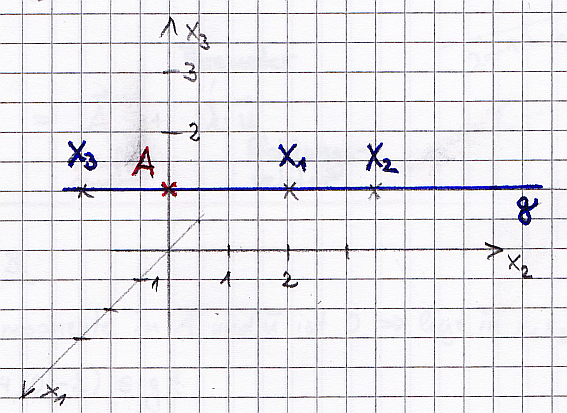
Eine Gerade im Raum

`g |\| x_2` (um 1 nach oben verschoben)


Ortsvektoren verschiedener Geradenpunkte
`vec X_0 = ((0),(0),(1)) = vec A`;   `vec X_1 = ((0),(2),(1))`;   `vec X_2 = ((0),(3.5),(1))`;   `vec X_3 = ((0),(-1.5),(1))`;


Ortsvektor allgemein
Ein Ortsvektor besteht offenbar
  • aus einem konstanten (`x_1` und `x_3`-Koordinate)
  • und einem variablen (`x_2`-Koordinate)
Teil. Versuche: `vec X = ((0),(0),(1))+lambda*((0),(1),(0))` wobei `lambda in RR`.
Je nach Belegung von `lambda` lassen sich so alle Punkte der Geraden darstellen.

Weitere Beobachtungen:
  • `((0),(0),(1))` stellt so etwas wie den Startpunkt,
  • `((0),(1),(0))` die Richtung der Geraden
dar.
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion