UHU-Startseite►Mathematik►Jahrgangsstufen►12►Anwendungen der Differential- und Integralrechnung►Fragen der Optimierung►Extremwertprobleme►
Dose, empirisch


Welche Abmessungen hat eine zylinderförmige 1-Liter-Dose bei minimaler Oberfläche?


a) Oberflächenformel und Abhängigkeiten
`O(r,h) = 2 pi r^2 + 2 pi r h`
  • ist von r und h abhängig
  • Für die Bestimmung der Minimalität ist eine Abhängigkeit von nur einer Variable anzustreben



b) Eliminierung der Höhe durch Nebenbedingung
Da es sich um 1-Liter-Dosen (Nebenbedingung!) handeln soll, muss folgende Gleichung erfüllt sein:
`V = 1 = pi r^2 h`
`=> h = 1/(pi r^2)`
also ist h(r) festgelegt und kann in O(r,h) eingesetzt werden:
`O(r) = 2 pi r^2 + 2/r = 2(pi r^2 + 1/r)`


c) Analyse des Funktionsterms
Betrachte das Verhalten an den Grenzen:
`lim_(r->0) pi r^2 -> 0`
`lim_(r->0) 1/r -> oo`

und

`lim_(r->oo) pi r^2 -> oo`
`lim_(r->oo) 1/r -> 0`
Der Graph steigt also an beiden Grenzen über jeden Wert hinaus, das Minimum befindet sich irgendwo dazwischen:



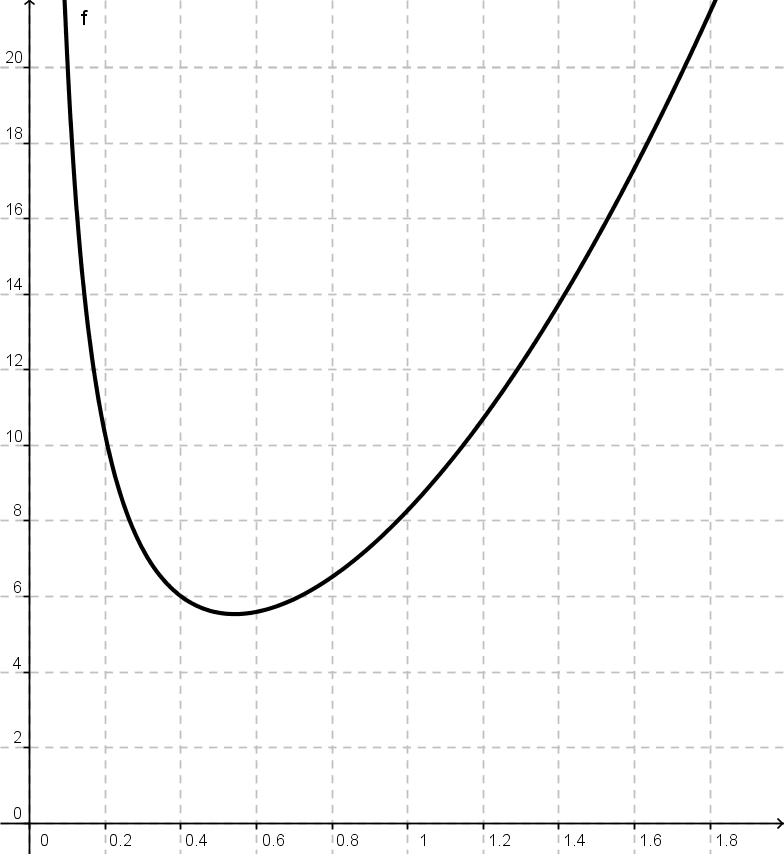
O(r)
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion