| Mäxchen |
Die sich ergebenden Zahlen werden so angeordnet:
31, 32, 41, 42, 43, 51, 52, 53, 54, 61, 62, 63, 64, 65, 11 (1er Pasch), 22 (2er Pasch), 33 (3er Pasch), 44 (4er Pasch), 55 (5er Pasch), 66 (6er Pasch) und 21(Mäxchen)
Zufallsgröße: `X: omega |-> text(Position im Spiel)`:
`31 |-> 1`, `32 |-> 2`, ... , `11 |-> 15`, ... `66 |-> 20`, `21 |-> 21`
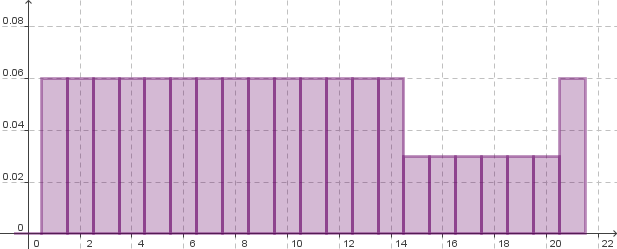
Wahrscheinlichkeitsverteilung: `text(Position im Spiel) |-> text(zugehörige Wahrscheinlichkeit)`:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| P(X=x) | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `2/36` | `1/36` | `1/36` | `1/36` | `1/36` | `1/36` | `1/36` | `2/36` |
| Chancen |
Da man durch Würfeln jeweils ein höheres Ergebnis als der Vorgänger erzielen muss lassen sich die eigenen Chancen leicht berechnen.
Angenommen, der Vorgänger hat einen 4er Pasch gewürfelt, dann kann man nur gewinnen, wenn man einen 5er, 6er Pasch oder ein Mäxchen würfelt:
`P(text(Gewinn)) = 1/36 + 1/36 + 2/36 = 4/36 = 1/9`.
| Vierblättrige Kleeblätter |
Zufallsexperiment: zweimaliges Ziehen eines Kleeblattes. Zufallsgröße: Anzahl der gezogenen vierblättrigen Glücksblätter. Erstelle eine Wahrscheinlichkeitsverteilung.
| Lösung (Teil I): Zufallsgröße |
| `omega` | `bar F bar F` | `bar F F` | `F bar F` | `F F` |
| x | 0 | 1 | 1 | 2 |
| Lösung (Teil II): Wahrscheinlichkeitsverteilung |
`P(F F) = 1/100*1/100 = 1/10000 = `0,01%
`P(bar F bar F) = 99/100*99/100 = 9801/10000 ~~` 98%
`P(bar F F) = P(F bar F) = 99/10000 ~~` 1%
| x | 0 | 1 | 2 |
| P(X=x) | 98% | 1%+1%=2% | 0% |