UHU-Startseite►Mathematik►Jahrgangsstufen►12►Binomialverteilung und Anwendung►Binomialkoeffizient, Binomialverteilung►Wahrscheinlichkeitsverteilungen►
Zufallsgrößen


Zwei einfache Zufallsexperimente
  1. Das Werfen einer Münze: `Omega = {W,Z}`
  2. Das Werfen von zwei Würfeln: `Omega = {(1|1),(1|2),...,(2|1),...(5|6),(6|6)}`
`Omega`: Ergebnisraum; `omega`: Ergebnis.


Eine Zahlzuordnung
Um rechnen zu können, ist es sinnvoll jedem Ergebnis eine eindeutige Zahl zuzuordnen:
  1. `W |-> 0` und `Z |-> 1`
  2. Jedem Paar wird seine Augensumme zugeordnet, also: `(1|1) |-> 2` ... `(6|6) |-> 12`
Solche Funktionen heißen Zufallsgrößen.


Eine Funktion X, die jedem Ergebnis `omega in Omega` eine reelle Zahl zuordnet heißt Zufallsgröße X.



Wahrscheinlichkeitsverteilung
Man erhält sie, wenn man jeder möglichen reellen Zahl ihre Wahrscheinlichkeit zuordnet
  1. Münzwurf:
    x01
    P(X=x)`1/2``1/2`
  2. Würfelsumme:
    x23456789101112
    P(X=x)`1/36``2/36``3/36``4/36``5/36``6/36``5/36``4/36``3/36``2/36``1/36`



Weg vom Experiment zur Verteilung
Insgesamt wird also jedem `omega in Omega` ein `x in RR` zugeordnet und diesem `x` wird wiederum ein `P(X=x)` zugeordnet:



Vom Experiment zur Wahrscheinlichkeitsverteilung

Graph der Wahrscheinlichkeitsverteilung
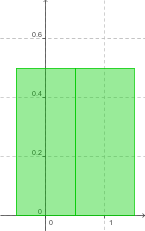
Betrachte den Graphen `x|->P(X=x)`. Da nur einzelnen x-Werten ein y-zugeordnet wird, ersetzt man den Punkt durch eine Säule der Breite 1:



Wahrscheinlichkeitsverteilung Münzwurf


Wahrscheinlichkeitsverteilung Würfelsumme
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion