Proportionalitäten als Funktion
| Die direkte Proportionalität als Funktion: Beispiel |
Für 1€ gibt es 1,40\$
für 2€ gibt es 2,80\$
... jedem Betrag in Euro wird also das 1,4 fache in Dollar zugeordnet:
x: Betrag in Euro; y: Betrag in Dollar;
`x|->1,4x`
`y=1,4x`
`f(x) = 1,4*x = 7/5 x`
| Der Graph der direkten Proportionalität |
- Da y und x immer im gleichen Verhältnis stehen, ist jedes Wertepaar vom Ursprung aus unter dem gleichen Winkel zu finden.
- Es ergibt sich eine Ursprungsgerade
-
zum zeichnen der Gerade:
- brauchst du zwei Punkte:
- den Ursprung
- und einen weiteren Punkt (im Beispiel 5 nach rechts, 7 nach oben)
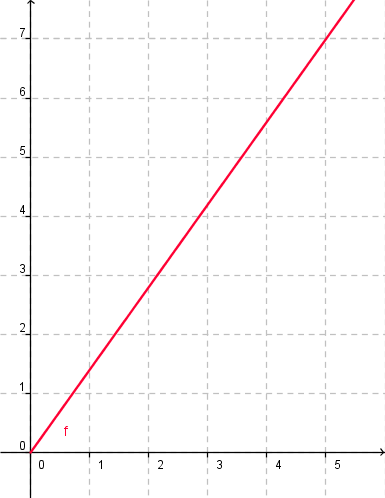
Dollarkurs als Funktion
| Die direkte Proportionalität als Funktion |
Allgemein: Die Funktionsgleichung `f(x) = m*x` stellt eine direkte Proportionalität dar.
`m` wird als Proportionalitätskonstante bezeichnet.
`m` wird als Proportionalitätskonstante bezeichnet.
| Bedeutung von m im Graphen |
`x|->1/10 x`
`x|->1/2 x`
`x|->5/4 x`
`x|->x`
`x|->3/2 x`
`x|->2 x`
`x|->3 x`
`x|->5 x`
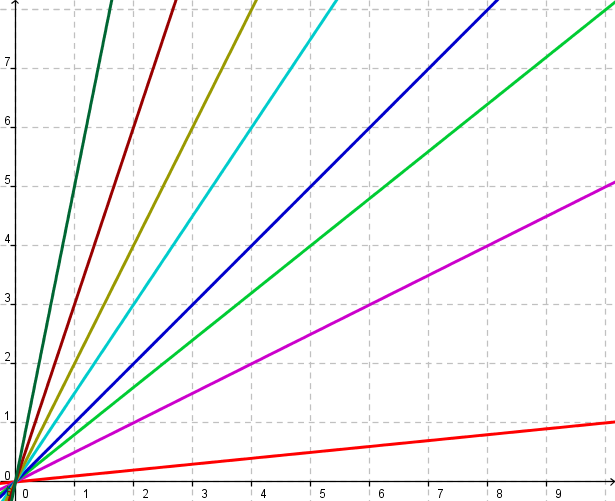
Graphen verschiedener Proportionalitäten
gehst du eins nach rechts, dann musst du 2 nach oben gehen
Beispiel `f(x) = 4/5 x`:
gehst du 5 nach rechts, dann musst du 4 nach oben gehen
Die Proportionalitätskonstante `m` gibt die Steigung `(Delta y)/(Delta x)` der Ursprungsgeraden an.
| Die indirekte Proportionalität als Funktion |
Allgemein: Die Funktionsgleichung `f(x) = a/x` stellt eine indirekte Proportionalität dar.
`a` ist die Proportionalitätskonstante der indirekten Proportionalität.