UHU-Startseite►Mathematik►Jahrgangsstufen►11►Anwendungen der ersten Ableitung►Monotonie und lokale Extremwerte►
Beispiele


1. kubische Funktion
`f(x) = 6 x^3 - 12 x^2 + 6 x` `x in RR`

a) Verhalten im Unendlichen:

`lim_(x->-oo) f(x) -> -oo` (`x^3`-Term ist negativ und wächst am schnellsten

`lim_(x->-oo) f(x) -> +oo` (`x^3`-Term ist positiv und wächst am schnellsten

b) Nullstellen:

`f(x) = 0 => 6 x *(x^2 - 2 x + 1) = 6 x * (x-1)^2 = 0`

`=> x_1 = 0`(einfach) und `x_2=1` (doppelt)

c) Monotonie und Extrempunkte:

`f'(x) = 18 x^2 - 24 x + 6`

`f'(x) = 0 => 6*(3 x^2 - 4x + 1) = 0`

Mitternachtsformel: `x_3 = 1/3; x_4 = 1`

VZT`x lt 1/3``x=1/3``1/3 lt x lt 1``x=1``1 lt x`
`f'(x)`+0-0+
`G_f`↗HOP↘TIP↗


Extrempunkte:

`f(1/3) = 8/9` und `f(1) = 0`

HOP `(1/3;8/9)` und TIP `(1;0)`

d) Graph:



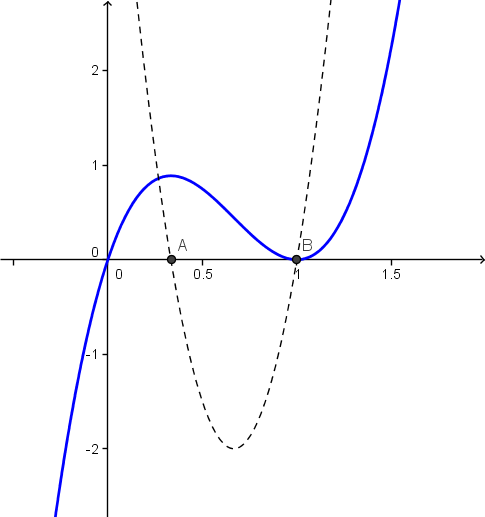
Monotoniebeispiel
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion