UHU-Startseite►Mathematik►Jahrgangsstufen►11►Anwendungen der ersten Ableitung►Newton-Verfahren►
graphisch


Berechnung von Nullstellen ganzrationaler Funktionen
Wie kommt man auf Nullstellen von ganzrationalen Funktionen, die eine höhere als die quadratische Ordnung besitzen?
[B] `f(x) = 1/3 x^3 +x^2 + 2 x +2/3`


Wie bekommt man die Nullstelle heraus?
`f(x) = 0 = 1/3 x^3 + x^2 + 2x + 2/3`
Mit den Schulverfahren lässt sich das nur bis `a x^2 + b x + c = 0` lösen.
Zur weiteren Analyse benötigt man eine Wertetabelle und den Graphen:
x`-2``-1``-1/2``0``1`
y`-2``-2/3``-1/3``+2/3``4`




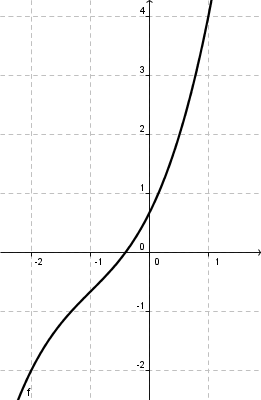
Graph einer ganzrationalen Funktion

Ausnutzung der Tangentensteigung
Schrittweise Annäherung mit Start bei `x_0=-2`. Wie könnte man mit Hilfe der Tangente im Punkt `T_1(-2|-2)` näher zur Nullstelle N gelangen?
  • Suche die Tangentengleichung in `T_1`
  • `x_1` ist Nullstelle der Tangente und näher an N




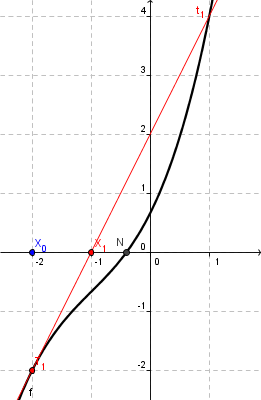
Funktion mit Tangente

Nimm nun `x_1=1` als Ausgangspunkt für den gleichen Prozess:
  • Bestimmung der Tangentengleichung für die Tangente im Punkt `(x_1,f(x_1))`.
  • Bestimmung ihrer Nullstelle ergibt `x_2`




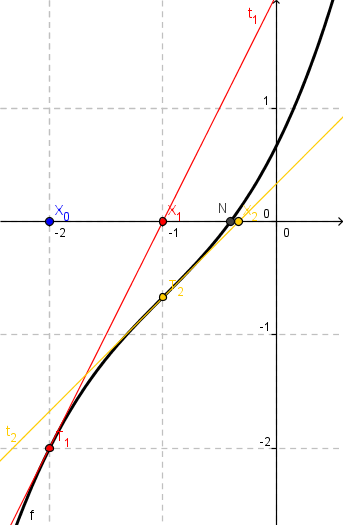
eine weitere Tangente an f

und jetzt das Ganze nochmal:



Die 3. Tangente an der Funktion
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion