Ein gleichwinkliges Dreieck ist gleichschenklig
| Kongruenzbeweis über das Einzeichnen der Höhe |
Satz: Wenn es in einem Dreieck zwei gleiche Winkel gibt, dann ist es gleichschenklig.
- Voraussetzung: Zwei Winkel eines Dreiecks sind gleich: `alpha=beta`
- Behauptung: Das Dreieck ist gleichschenklig
-
Beweis:
- Hilfslinie: Lot von C auf [AB] ergibt den Schnittpunkt M
- Betrachte die entstandenen Teildreiecke `Delta AMC` und `Delta BMC`
- `bar(MC) = bar(MC)`
- ` 90° = 90°`
- `alpha = beta`
- `Delta AMC` ~= `Delta BMC` (WWS)
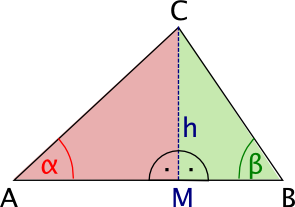
Grafik zum Kongruenzbeweis
| Kongruenzbeweis über das Einzeichnen der Winkelhalbierenden bei C |
- Voraussetzung: Zwei Winkel eines Dreiecks sind gleich `alpha = beta`
- Behauptung das Dreieck ist gleichschenklig
- Beweis:
- Hilfslinie: Winkelhalbierende bei C auf [AB] ergibt den Schnittpunkt M
- Betrachte die entstandenen Teildreiecke `Delta` AMC und `Delta` BMC:
- `gamma_1 = gamma_2`
- `bar(MC) = bar(MC)`
- `alpha = beta`
- `Delta`AMC `~= Delta`BMC (WWS)
| Kongruenzbeweis über das Einzeichnen der Seitenhalbierenden |
- Voraussetzung: Zwei Winkel eines Dreiecks sind gleich `alpha = beta`
- Behauptung das Dreieck ist gleichschenklig
- Beweis:
- Hilfslinie: Seitenhalbierende von C auf [AB] ergibt den Schnittpunkt M
- Betrachte die entstandenen Teildreiecke `Delta` AMC und `Delta` BMC:
- `bar(AM) = bar(BM)`
- `bar(MC) = bar(MC)`
- `alpha = beta`
- `Delta`AMC `~= Delta`BMC (SsW)