| ► | Ein gleichwinkliges Dreieck ist gleichschenklig | |
| ► | Satz von Thales |
Das Beweisen
| Die Notwendigkeit von Beweisen |

Die beiden roten Strecken sind kongruent

Die zwei übereinanderliegenden Figuren sind kongruent
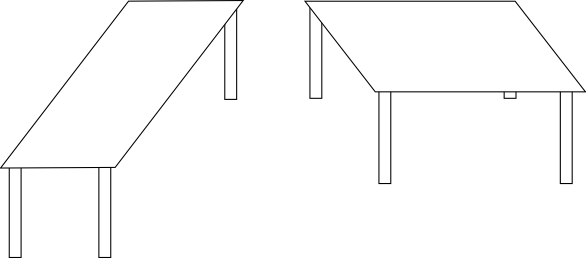
Die zur Darstellung der Tischplatte gezeichneten Parallelogramme sind kongruent
| Über das Beweisen im aktuellen Lehrplan |
- Da im aktuellen Lehrplan das Formale eine geringere Rolle spielt, ist der Beweis in seiner strengen Form nicht mehr vorhanden
- Zum Ausgleich wird aber darauf bestanden, Kausalitäten allgemein mehr in den Vordergrund zu stellen
- und auf die Notwendigkeit logischer Argumentation immer wieder hinzuweisen (z.B. im Zusammenhang mit dynamischen Geometriesystemen)
- entsprechender Abschnitt des Lehrplans
| Beispiel: Satz und Kehrsatz |
- Analysiere Aussagen aus der Mathematik oder aus deinem Umfeld:
''Bei Regen ist Theo zu spät''
''Die Gegenseiten eines Parallelogramms sind jeweils gleichlang''
- Bringe sie in die ''Wenn-Dann-Form'':
''Wenn es regnet, dann ist Theo zu spät''
''Wenn ein Viereck ein Parallelogramm ist, dann sind die Gegenseiten jeweils gleichlang''
- Formuliere jeweils Voraussetzung und Behauptung:
Voraussetzung: ''es regnet'', Behauptung:''Theo kommt zu spät''
Voraussetzung: ''ein Viereck ist Parallelogramm'', Behauptung:''die Gegenseiten sind jeweils gleichlang''
- Kehrsatz:
entsteht durch die Vertauschung von Voraussetzung und Behauptung:
''Wenn Theo zu spät kommt, dann regnet es''
''Wenn zwei gegenüberliegende Seiten jeweils gleichlang sind, dann ist ein Viereck ein Parallelogramm''
- Wird in einem Satz die Voraussetzung mit der Behauptung vertauscht, so entsteht ein neuer Satz. Er heißt Kehrsatz zum ursprünglichen Satz. Die Vertauschung von Voraussetzung und Behauptung nennt man Satzumkehrung.