Einführung Wurzelfunktion


Aufhänger
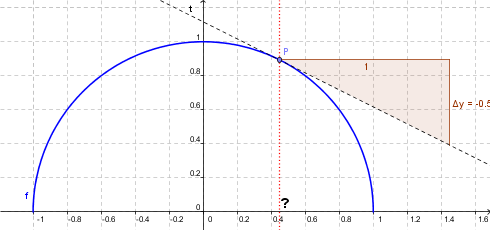
Ein armer Mensch muss auf einer Kuppel (Radius 1m) Schnee schieben. Aus Sicherheitsgründen darf er sich aber nicht weiter als bis zu einer Steigung von 50% „hinauswagen“. Berechne seinen den maximalen Abstand von der Rotationsachse.
Gesucht ist die Ableitungsfunktion der „Kuppelfunktion“.
Die Kuppel kann durch einen Halbkreis beschrieben werden:
Nach Pythagoras gilt für jeden Punkt der Funktion:`x^2+y^2=1`
Auflösen nach y ergibt`y = k(x) = sqrt(1 - x^2)`
mit der Definitionsmenge: `D_f = [-1;+1]`



Einfacher Aufhänger
Wenn die Wurzelfunktion als Umkehrfunktion der quadratischen Funktion eingeführt wurde, dann kann man auch schön geometrisch über die senkrechte Tangente am Scheitelpunkt motivieren.



Kuppelfunktion

Ableitung der Wurzelfunktion
Umbau in Potenzschreibweise: `f(x) = sqrt(x) = x^(1/2)`
führt zu der Vermutung: `f'(x) = 1/2*x^(-1/2)`
Begründung:
Setze `g(x) = x = (f(x))^2`
Dann gilt:`g'(x) = 1 = 2*f(x)*f'(x)`
Auflösen nach `f'(x)`: `f'(x) = 1/(2*f(x)) = 1/(2 sqrt x)`
mit der Voraussetzung, dass `f'(x)` existiert.
Wenn `f(x) = sqrt x` dann ist
`f'(x) = 1/(2 sqrt x)` mit `x in RR^text(+)`



Unbedingt zu beachten:
Diese Ableitung erfolgt über die Identität von zwei Funktionen. Daher muss die Bedeutung des Gleichheitszeichens geklärt werden und anschließend andiskutiert werden, warum bei identischen Funktionen deren Ableitungsfunktionen ebenfalls identisch sind (Steigungsverhalten der Graphen).


Ableitung der Kuppelfunktion
`k(x) = sqrt(1 - x^2)`
`k'(x) = 1/(2 sqrt(1-x^2))*(-2x) = -x/sqrt(1-x^2)`
`k'(x) = -1/2 = x/sqrt(1-x^2) => -1/2 sqrt(1-x^2) = x`
`1/4 (1-x^2) = x^2`
`1/4 - 1/4 x^2 = x^2`
`1 - x^2 = 4 x^2`
`1 = 5 x^2`
`x = +- 1/sqrt 5 ~~ 0.45`


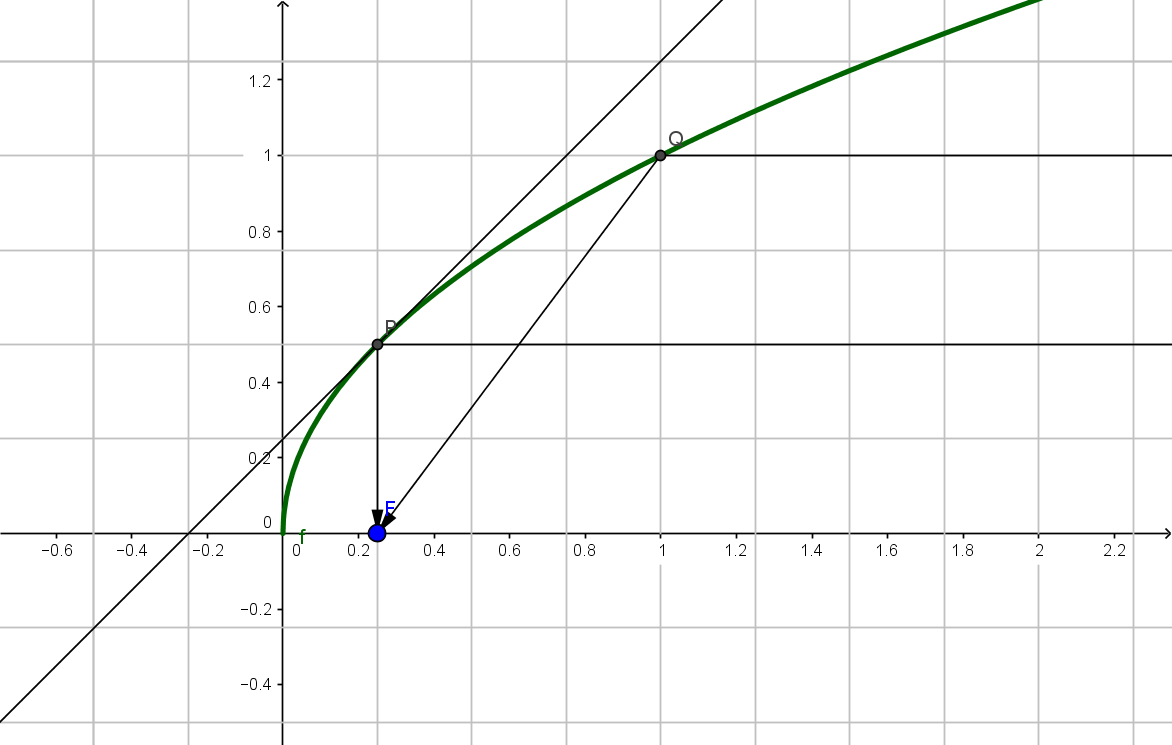
Alternative: Reflexionsgesetz an Parabolspiegel
Ein Parabolspiegel ist im Koordinatensystem "nach rechts" ausgerichtet. Seine Symmetrieachse stimmt also mit der x-Achse überein. Zur Bestimmung des auf der Symmetrieachse liegenden Brennpunktes sucht man denjenigen parallel zur x-Achse einfallenden Lichtstrahl, der bei Spiegelung senkrecht nach unten abgelenkt wird.

Mit Hilfe des Reflexionsgesetzes aus der Physik sucht man also denjenigen Punkt des Graphen, bei dem die Tangentensteigung 45° beträgt:

$f'(x) = 1$

Wenn die Ableitungsfunktion bekannt ist, dann gilt:

$\frac 1 {2 \sqrt x} = 1\Rightarrow \sqrt x = \frac 1 2\Rightarrow x = \frac 1 4$

Dann überprüfen, ob ein weiterer parallel einfallender Lichtstrahl in diesem Brennpunkt ankommt. Beispielsweise derjenige, der bei $x=1$ auf den Spiegel trifft:

$f'(1)$ berechnen ($f'(1)=\frac 1 2$), den Winkel ausrechnen, verdoppeln und die zugehörige Steigung berechnen.

$m =\frac 4 3$. Trägt man von $(1;1)$ aus eine Gerade mit dieser Steigung an, so geht diese ebenfalls durch den Brennpunkt.



Parabolspiegel mit Wurzelfunktion