Einführungsstunde 2010
| Grundstruktur |
- Schüler ermitteln Tangenten und deren Steigung arbeitsteilig grafisch
- Eine Vermutung wird geäußert
- Die Vermutung wird mittels Geogebra visuell untermauert
- Die Ableitung der Kosinusfunktion wird über die Ableitung der verschobenen Sinusfunktion hergeleitet
| Darstellung der Tangentensteigungen mittels geogebra |
Idee:
- Definition eine Liste von Punkten auf dem Graphen der Sinusfunktion
- Bildung einer Liste von Sekanten
- Darstellung einer Liste von Punkten für die Sekantensteigungen
- Verringerung des Punktabstandes
| Geogebra-Konstruktionsprotokoll |
| Nr. | Name | Definition | Algebra |
|---|---|---|---|
| 1 | Zahl h | h = 2 | |
| 2 | Liste Liste1 | Folge[i h, i, -50, 50] | Liste1 = {-100, -98, ... 98, 100} |
| 3 | Funktion f | f(x) = sin(x) | |
| 4 | Liste Liste2 | Folge[(Element[Liste1, i], f(Element[Liste1, i])), i, 1, 101] | Liste2 = {(-100, 0.51), (-98, 0.57), ... (100, -0.51)} |
| 5 | Liste Liste3 | Folge[((Element[Liste1, i] + Element[Liste1, i + 1]) / 2, (y(Element[Liste2, i + 1]) - y(Element[Liste2, i])) / h), i, 1, 100] | Liste3 = {(-99, 0.03), (-97, -0.78), ... (99, 0.03)} |
| 6 | Punkt P | Element[Liste2, 51] | P = (0, 0) |
| 7 | Punkt Q | Element[Liste2, 52] | Q = (2, 0.91) |
| 8 | Gerade a | Gerade durch P, Q | a: -0.91x + 2y = 0 |
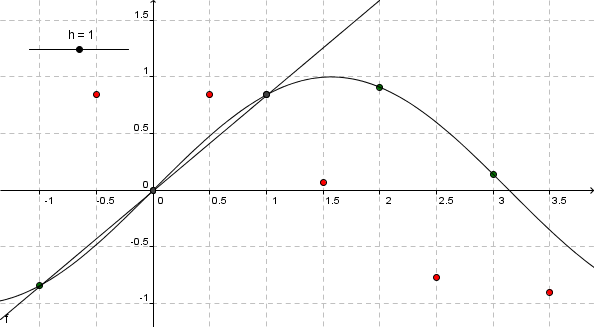
Differenzenquotient sin(x) mit h=1
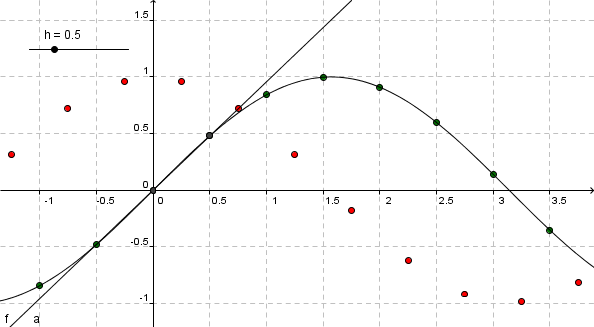
Differenzenquotient sin(x) mit h=0.5
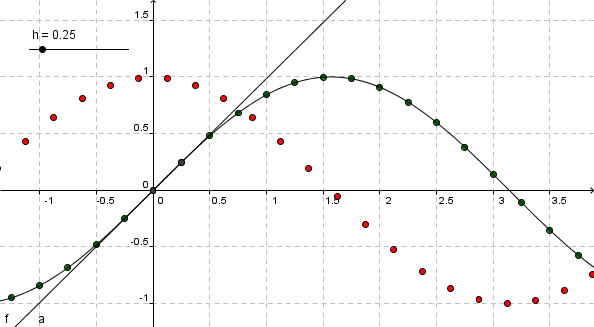
Differenzenquotient sin(x) mit h=0.25
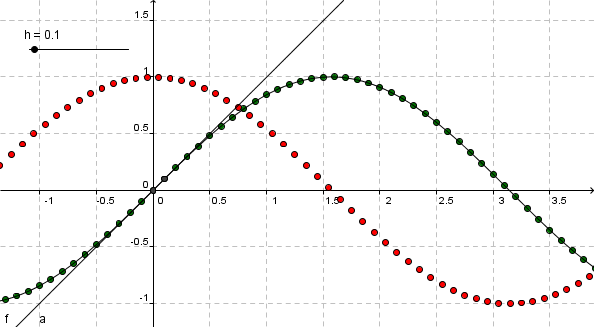
Differenzenquotient sin(x) mit h=0.1
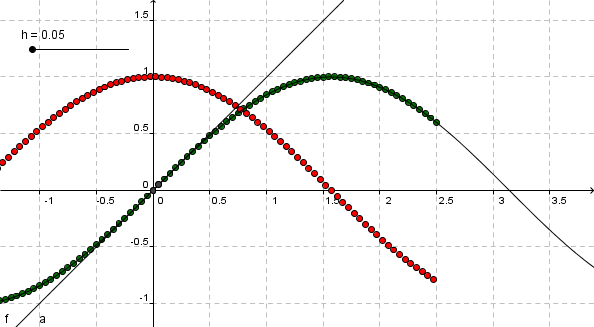
Differenzenquotient sin(x) mit h=0.05