Satz des Thales


Methodische Vorüberlegungen nach "http://de.wikipedia.org":
Formulierung des Satzes:
  • Konstruiert man ein Dreieck aus den beiden Endpunkten des Durchmessers eines Halbkreises (Thaleskreis) und einem weiteren Punkt dieses Halbkreises, so erhält man immer ein rechtwinkliges Dreieck.
  • Oder: Liegt der Punkt C eines Dreiecks ABC auf einem Halbkreis über der Strecke AB, dann hat das Dreieck bei C einen rechten Winkel.
Es reicht durchaus, diese eine Richtung des Satzes in einer Stunde durchzunehmen.


Beweis
Ein Beweis läuft über das Zerlegen des Dreiecks in zwei gleichschenklige Teildreiecke:



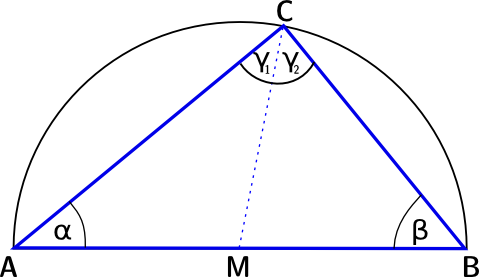
Beweis des Satzes von Thales

Linkes Teildreieck gleichschenklig: `r=bar(MA)=bar(MC) => alpha = gamma_1`
Rechtes Teildreieck gleichschenklig: `r=bar(MB)=bar(MC) => beta = gamma_2`
Winkelsumme im Dreieck:
`alpha + beta + gamma_1 + gamma_2 = 180°`
`alpha + beta + alpha + beta = 180°`
`2 (alpha + beta) = 180°`
`=> alpha + beta = 90°`
Winkelsumme: `gamma = 180°-(alpha + beta) = 90°`     `sqrt`


Umkehrung
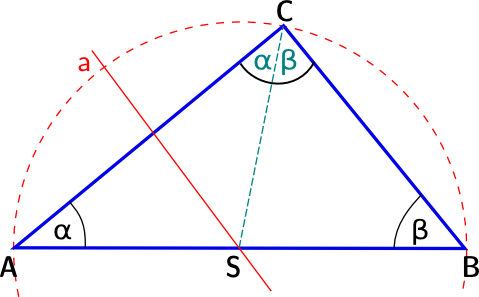
Verbindet man die geometrischen Orte aller Punkte von denen aus eine gegebene Strecke [AB] unter einem 90°-Winkel erscheint, so erhält man zwei Halbkreise +ber [AB].



Beweis der Umkehrung des Satzes von Thales

Beweis der Umkehrung des Satzes von Thales
Voraussetzung: der Winkel bei C ist 90°. Wegen der Winkelsumme im Dreieck muss dann auch gelten: `alpha+beta = 90°`.
a soll die Symmetrieachse der Strecke [AC] sein.
S ist der Schittpunkt aus a und [AB].
S ist also von A und C gleichweit entfernt: `bar(SA) = bar(SC)`.
Dann ist das Dreieck `Delta ASC` gleichschenklig.
Also ist der Winkel dieses Teildreieckes bei C wieder `alpha`.
Wegen `alpha + beta = 90°` muss außerdem der andere Teilwinkel bei C `beta` sein.
Also erhält man mit S zwei gleichschenklige Teildreiecke und es gilt:
`bar(SA) = bar(SC) = bar(SB)`, also liegen A, B und C auf einem Kreis um S.   `sqrt`.