Fehlerwahrscheinlichkeit bei bekannter Verteilungsfunktion


Situation
  • Ein Hersteller will 100 000 Knallkörper an den Mann bringen und behauptet (Hypothese!)
  • Ausfallwahrscheinlichkeit: 4%
Zur Überprüfung wird eine
  • Stichprobe mit 200 Knallkörpern durchgeführt
  • Die Hypothese wird bei 13 oder mehr defekten Knallkörpern verworfen
Wie groß ist der Fehler 1. Art `alpha` (WS dass Hypothese stimmt und trotzdem verworfen wird)?


Binomialverteilung
Jeder einzelne Versuch aus der Stichprobe wird (nahezu) unter den gleichen Bedingungen ausgeführt, ein Treffer hat bei jedem Versuch die gleiche Wahrscheinlichkeit p.
`=>` es handelt sich um eine Bernoullikette
`=>` für jede Trefferzahl k bei n Versuchen gibt es eine feste Wahrscheinlichkeit:
`P_p^n(X=k)=B(n;p;k) = ((n),(k)) p^n (1-p)^(n-k)`.
Trägt man alle Wahrscheinlichkeiten über der Trefferzahl auf, so erhält man die Binomialverteilung:



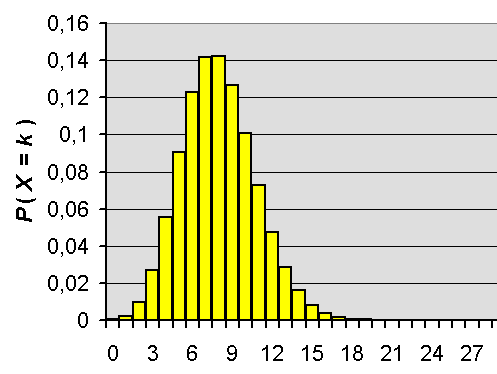
Beispiel für die Binomialverteilung bei n=200 und p=0,04

Fehlerwahrscheinlichkeit: Beispiel
Berechnung des Fehlers 1. Art im Knallkörperbeispiel:
`n = 200; H_0: p = 0.04; k >= 13`



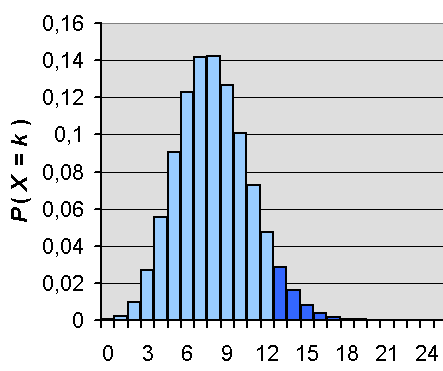
Alle Wahrscheinlichkeiten für die Ablehnung bei p=0,04

Der Wert des Fehlers ergibt sich durch Summierung der Wahrscheinlichkeiten aller Fälle für `k >= 13`:
`alpha = B(200;13;0,04)+B(200;14;0,04)+...+B(200;200;0,04) = 2.87% + 1.60% + ... = 5.99%`



Nachschlagen des Fehlers im Tabellenwerk
  • Die aufsummierten Wahrscheinlichkeiten sind für verschiedene Parameter im Tabellenwerk ausgedruckt
  • Da die Summe aller Werte 1 ergibt, sind nur Werte angegeben, die von k=0 an aufsummiert wurden
  • Daher ist für den Bereich `13 le k le 200` eine Umrechnung notwendig:
    `P_0.04^200(13 le Z) = 1-P_0.04^200(Z lt 13) = 1-0.9401 = 0.0599`,
    da die Summe aller Trefferwahrscheinlichkeiten (sicheres Ereignis) 1=100% ergibt.




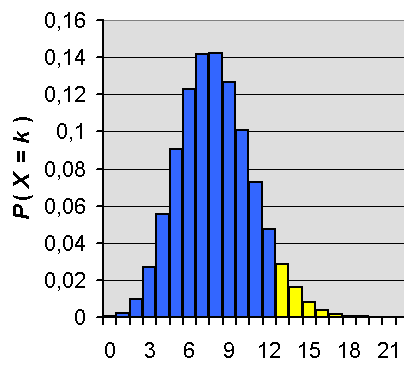
Summe der WS von 0 bis 12