UHU-Startseite►Mathematik►Jahrgangsstufen►8►Elementare gebrochen-rationale Funktionen►Einfache Bruchgleichungen►
Lösen einer einfachen Bruchgleichung


Beispiel Linsengleichung
`1/(x)+1/x = 1/f`Bruchgleichung
`D = QQ "\" {0}`Definitionsmenge bestimmen
`HN = f*x`Hauptnenner (HN) bestimmen
`1/(x)+1/x = 1/f |*f*x`mit HN durchmultiplizieren
`(f*x)(1/(x)+1/x) = (f*x)*1/f`
`(f*x)/(x)+(f*x)/x = (f*x)/f`Distributivgesetz anwenden
`f+f = x`kürzen
`x = 2f`ausrechnen
`x in D`mit D vergleichen
`L = {2f}`L angeben
Lösung der entsprechenden Situation an der Sammellinse: Der Gegenstand muss auf die doppelte Brennweite von der Linse entfernt werden, dann ist das Bild ebenfalls bei der doppelten Brennweite.


Beispiel 2
`1/(2x) + 1/x = 3`
`D = QQ text(\) {0}
`HN = 2*x`
`(2x)/(2x) + (2x)/x = 2x*3`
`1 + 2 = 6x`
`3 = 6x`
`x = 1/2`
`x in D => L = {1/2}`


Beispiel 3: Wo treffen sich zwei gebrochen rationale Funktionen?
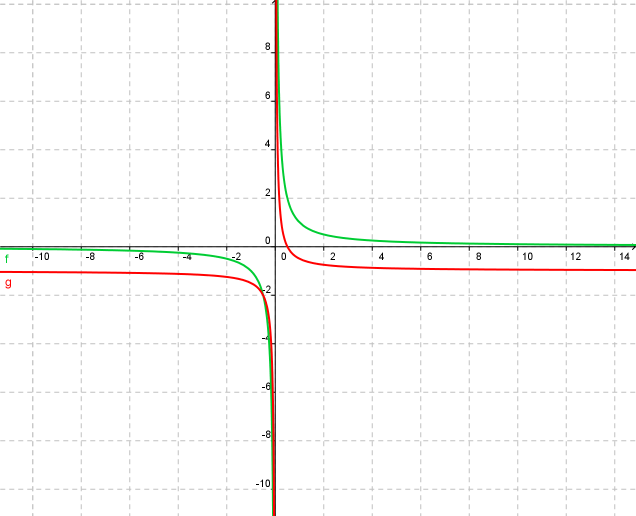
`f(x) = 1/x` und `g(x) = 1/(2x)-1`, gesucht sind alle Schnittpunkte



Schnittpunkt zweier gebrochen rationaler Funktionen

`1/x = 1/(2x) - 1`
`D = QQ text (\) {0}`
`HN = 2*x`
`(2x)/x = (2x)/(2x) - 2x`
`2 = 1 - 2x`
`2x = -1`
`x = -1/2`
auf welcher "Höhe" treffen sie sich? `f(-1/2) = 1/(-1/2) = 1:(-1/2) = 1*(-2/1) = -2`
Schnittpunkt: `S(-1/2|-2)` wie in der Zeichnung erkennbar.
optimal sichtbar mit Firefox Formeln mit asciimath Druckversion