UHU-Startseite►Mathematik►Jahrgangsstufen►9►Trigonometrie am rechtwinkligen Dreieck►
Sinus und Kosinus als Seitenverhältnis im rechtwinkligen Dreieck


Dreiecke mit Hypothenusenlänge ungleich 1
    Sinus und Kosinus sind für rechtwinklige Dreiecke mit Hypothenusenlänge 1 definiert. Wie rechnet man auf andere Hypothenusenlängen um?




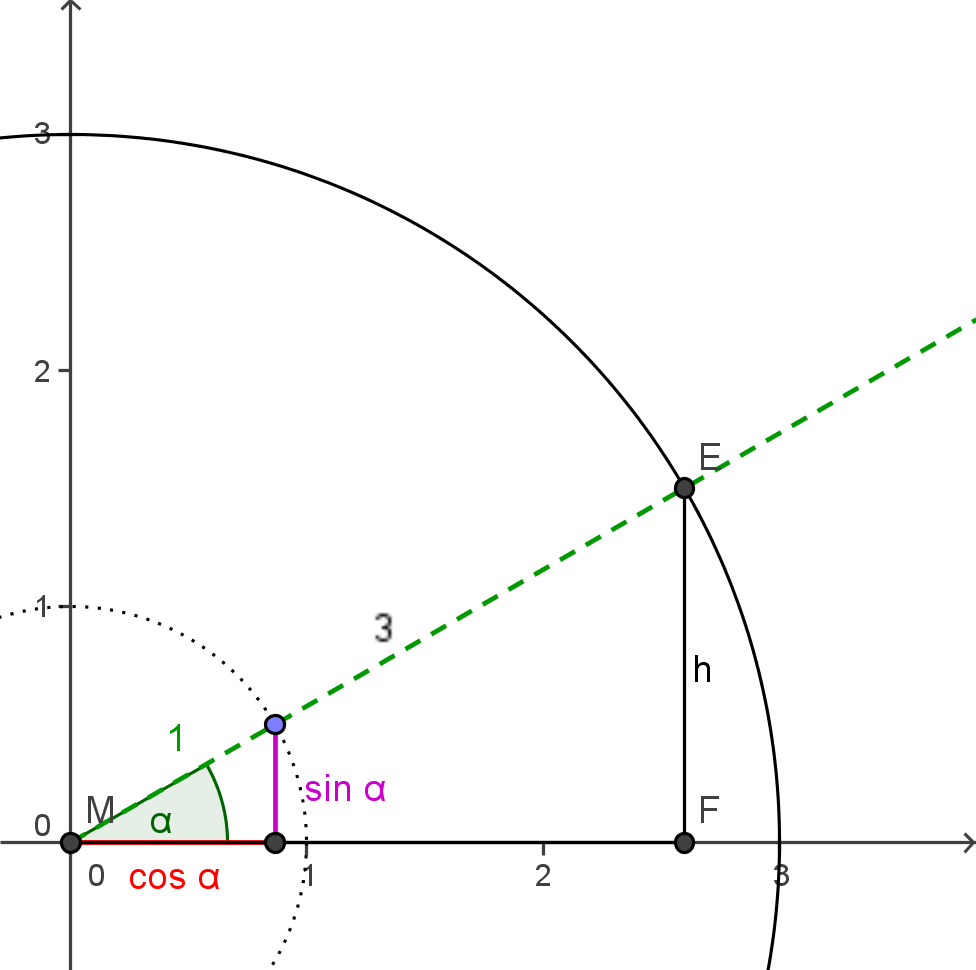
Berechnung von Sinus und Kosinus bei Hypothenusenlänge 3

Berechnung von Kathetenlängen in rechtwinkligen Dreiecken
  • `Delta MFE` ist ähnlich zum Einheitsdreick
  • `=>` Streckenverhältnisse bleiben gleich
`(sin alpha)/1 = h/3` oder allgemein:
`(sin alpha)/1 = "Gegenkathetenlänge"/"Hypothenusenlänge"`
`(cos alpha)/1 = bar( MF )/3` oder allgemein:
`(cos alpha)/1 = "Ankathetenlänge"/"Hypothenusenlänge"`



Sinus und Kosinus im rechtwinkligen Dreieck
`sin alpha = text(Gegenkathete)/text(Hypothenuse)`
`cos alpha = text(Ankathete)/text(Hypothenuse)`
(hier sind mit Kathete und Hypothenuse die Länge der jeweiligen Dreiecksseite gemeint)



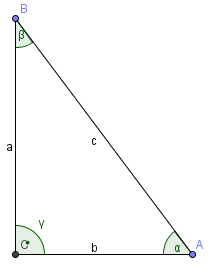
Rechtwinkliges Dreieck

Aufgaben
  1. In einem Dreieck ist c = 10, α = 70°, γ = 90°. Bestimme sämtliche Seitenlängen und Winkel.
  2. In einem rechtwinkligen Dreieck ist a = 12 und b = 5. Bestimme sämtliche Größen des Dreiecks.



Lösungen
  1. `beta = 180° - gamma - alpha = 20°`
    `sin alpha = a/c => a = sin alpha * c = 0.94*10 = 9.4`
    `cos alpha = b/c => b = cos alpha * c = 0.34*10 = 3.4`
  2. `c = sqrt( a^2 + b^2 ) = sqrt( 144 + 25 ) = sqrt 169 = 13`
    `sin alpha = a/c => alpha = arcsin(a/c) = 67.4°`
    `beta = 90° - alpha = 23.6°`



Kartenaufgabe
In einem rechtwinkligen Dreieck ist
  1. c=12, γ = 90° und β = 10°.
  2. a = b, γ = 90° und α = 45°.
  3. a = 3, b=4 und c = 5
Bestimme alle Größen.


Tipp A
  1. Bestimme zuerst α über die Winkelsumme und wende anschließend Sinus oder Kosinus an
  2. Das Dreieck ist gleichschenklig (symmetrisch).
  3. Welcher Winkel ist 90°. Bestimme die anderen mit Sinus und Kosinus.



Tipp B
  1. `alpha = 80°; sin α = a/c;`
  2. `beta = 45°`; Lassen sich die Längen der Seiten vollständig bestimmen, oder muss eine Seitenlänge vorgegeben werden?`
  3. `γ = 90°; sin α = a/c; cos α = b/c



Lösung
  1. `alpha = 80°, beta = 10°, gamma = 90°`
    `sin alpha = a/c => a = sin alpha * c = 11.82; cos alpha = b/c => b = 2.08; c = 12`
  2. `alpha = beta = 45°; gamma = 90°`
    a ist frei wählbar, z.B. a = 1
    `=> b = a = 1 => c = sqrt(1^2 + 1^2) = sqrt 2`
  3. `sin alpha = a/c = 0.6 => alpha = 36.87°, beta = 90°-36.87° = 53.13°, gamma=90°`
    `a = 3, b = 4, c = 5`



Kartenaufgabe II
Aristarch von Samos bestimmte bei Halbmond die Entfernung Erde-Sonne aus der Entfernung Erde-Mond (384 000 km) und dem Winkel, unter dem Halbmond und Sonne erscheinen.
  1. Aristarch bestimmte den Winkel zu 87°. Welche Entfernung hatte seiner Rechnung nach die Sonne?
  2. Die tatsächliche Entfernung der Sonne beträgt `149*10^6 km`. Bestimme den tatsächlich vorhandenen Winkel, den Halbmond und Sonne am Himmel miteinander einschließen.



Tipp A zu KA II
Zeichne die Stellung von Erde, Sonne und Mond in einem Dreieck auf. Welcher Winkel befindet sich in diesem Dreieck beim Mond, wenn es sich um Halbmond handelt?


Tipp B zu KA II
Beim Mond befindet sich ein 90°-Winkel. Die Entfernung Erde-Mond ist bekannt. Also lässt sich die Entfernung Erde-Sonne über eine Winkelfunktion berechnen.



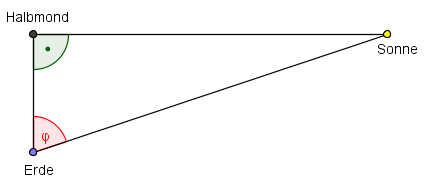
Erde-Sonne-Mond bei Halbmond

Lösung zu KA II
  1. `cos phi = bar(EM)/bar(ES) => bar(ES) = bar(EM)/(cos phi) = (384 000 km)/0.05234 = 7.3*10^6 km`
  2. `cos phi = bar(EM)/bar(ES) = (384 000 km)/(149*10^6 km) = 0.00258 => phi = 89.85°`


optimal sichtbar mit Firefox Formeln mit asciimath Druckversion