Einführung über "Schere, Stein, Papier"


Das Spiel
  • Zwei Kontrahenten spielen gegeneinander
  • Entscheiden sich für eines der Symbole "Schere", "Stein" oder "Papier"
  • Das Symbol wird mit der Hand dargestellt
  • Gewonnen hat der, dessen Symbol dem des anderen übergeordnet ist:
    • Schere schneidet Papier
    • Papier wickelt den Stein ein
    • Stein schleift die Schere



Das Laplace-Modell
Auch wenn ein Mensch sich nicht genau zu `1/3` für eines der Symbole entscheidet, so kann man dies ja einmal annehmen (typisch Mathematiker) und die Wahl von Person A und Person B in einem Baum darstellen:



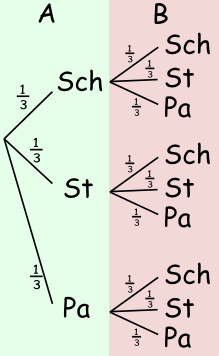
Ein Baum für Schere, Stein, Papier

Fragen zum Baum
  1. P("Papier trifft auf Papier")
  2. P("A gewinnt")



Antworten
    • in `1/3` aller Fälle wählt A Papier
    • in `1/3` dieser 'A-Papier-Fälle' wählt auch B Papier
    • also trifft in `1/9` aller Fälle Papier auf Papier
    • P("Papier trifft auf Papier") = `1/3*1/3=1/9`
  2. A gewinnt in folgenden Fällen:
    • P("PapierA-SteinB")=`1/9`
    • P("SteinA-SchereB")=`1/9`
    • P("SchereA-PapierB")=`1/9`
    3 verschiedene Fälle mit jeweils `1/9` Wahrscheinlichkeit führen zum Sieg, die Gesamtchance steigt also entsprechend:
    P(A gewinnt) = `1/9 + 1/9 + 1/9 = 1/3`



Nachteil
Dieses Beispiel ist zu symmetrisch!


Schere-Stein-Papier-Brunnen
Betrachte das Baumdiagramm und beantworte folgende Fragen:
  • Wie groß sind die WS für A gewinnt, verliert oder Unentschieden?
  • Wo siehst du etwas besonderes?




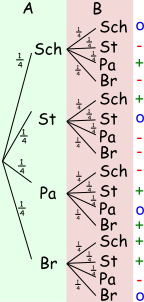
Ein Baum für Schere, Stein, Papier und Brunnen