Ableitungsfunktion als Indikator
| Monotoniekriterium |
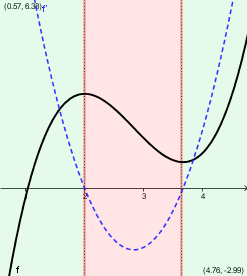
Ableitungsfunktion und Monotonie
MONOTONIEKRITERIUM
ist `f'(x) > 0` für alle `x in [a;b]` so ist `f` dort streng monoton steigend.
ist `f'(x) < 0` für alle `x in [a;b]` so ist `f` dort streng monoton fallend.
ist `f'(x) > 0` für alle `x in [a;b]` so ist `f` dort streng monoton steigend.
ist `f'(x) < 0` für alle `x in [a;b]` so ist `f` dort streng monoton fallend.
| Extremwertkriterium |
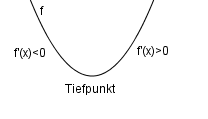
Tiefpunktkriterium
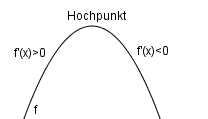
Hochpunktkriterium
Ist f in der Umgebung von `x_0` diffbar und wechselt bei `x_0` das Vorzeichen, so besitzt der Graph dort einen Extremwert.
Maximum: f'(x) wechselt von + nach -
Minimum: f'(x) wechselt von - nach +
Maximum: f'(x) wechselt von + nach -
Minimum: f'(x) wechselt von - nach +