|
Numerische Berechnung von Grenzwerten
| Tangentensteigung von sin(x) im Nullpunkt |
Wie groß ist die Steigung der Tangente der Funktion f(x) = sin(x) im Nullpunkt?
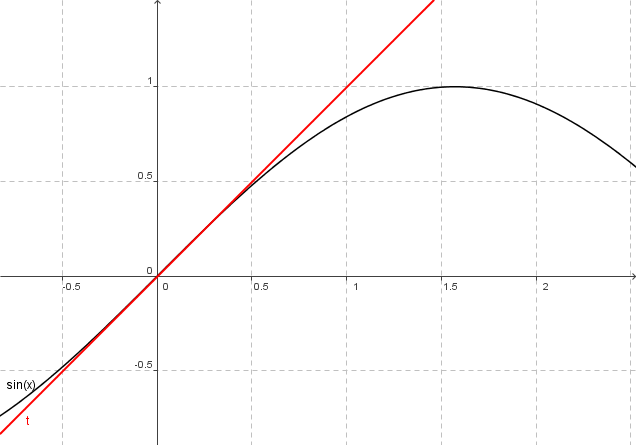
Sinusfunktion mit Tangente im Nullpunkt
| Bildung des Differenzenquotienten |
Ausgehend vom Nullpunkt soll die Steigung der Sekante berechnet werden:
`(f(0+h)-f(0))/h = (sin(0+h)-sin(0))/h = (sin(h)-sin(0))/h = sin(h)/h`
In diesem Term lässt h sich nicht kürzen, man kann also nicht unmittelbar h = 0 setzen. Stattdessen kann man versuchen, den Grenzwert zu erreichen, indem man die Entwicklung des Termwertes für immer kleiner werdendes h untersucht:
| h | sin(h) | `sin(h)/h` |
| 0,5 | 0,479425539 | 0,958851077 |
| 0,2 | 0,198669331 | 0,993346654 |
| 0,1 | 0,099833417 | 0,998334166 |
| 0,05 | 0,049979169 | 0,999583385 |
| 0,02 | 0,019998667 | 0,999933335 |
| 0,01 | 0,009999833 | 0,999983333 |
| 0,005 | 0,004999979 | 0,999995833 |
| 0,002 | 0,001999999 | 1 |
| 0,001 | 0,001 | 1 |
Also gilt: `lim_(h->0)sin(h)/h = 1`
| h | sin(h) | `sin(h)/h` |
| -0,5 | -0,479425539 | 0,958851077 |
| -0,2 | -0,198669331 | 0,993346654 |
| -0,1 | -0,099833417 | 0,998334166 |
| -0,05 | -0,049979169 | 0,999583385 |
| -0,02 | -0,019998667 | 0,999933335 |
| -0,01 | -0,009999833 | 0,999983333 |
| -0,005 | -0,004999979 | 0,999995833 |
| -0,002 | -0,001999999 | 1 |
| -0,001 | -0,001 | 1 |
Also gilt auch für negative h: `lim_(h->0)sin(h)/h = 1`
|
